Все продукты | Schneider Electric Украина

Доступ к энергии

Автоматизация и безопасность зданий

Системы резервного питания и охлаждения

Автоматизация и промышленный контроль

se.com/ua/ru/work/products/low-voltage-products-and-systems/»>

Распределение электроэнергии низкого напряжения

Распределение электроэнергии среднего напряжения и автоматизация электроснабжения

Электроустановочное оборудование и системы управления домом

Солнечная энергетика

U.

S.A.F. B-2A Spirit Stealth Bomber, Modelcollect UA72201 (2017)

Modelcollect | Нет. UA72201 | 1:72

Факты

Фирма:

Modelcollect

Заголовок:

U.S.A.F. B-2A Spirit Stealth Bomber

Число:

UA72201

Масштаб:

1:72

Тип:

Полный набор

Вышел:

2017 | Первый выпуск — новый комплект

Штрих-код:

4250580581598 (EAN)

Тема:

Northrop B-2 Spirit » Реактивные (Авиация)

Обозначения

Northrop B-2 Spirit

Northrop B-2A Spirit

US Air Force (1947-now)

• 509 BW 82-1066/Spirit of America
  Март 2012 — Whiteman AFB, MO
  FS17875 FS36118
• 509 BW, 13 BS 82-1071/Spirit of Mississippi
  Октябрь 2004 — Whiteman AFB, MO
  FS17875 FS36118
• 509 BW, 13 BS 82-1068/Spirit of New York
  Июль 2012 — Whiteman AFB, MO
  FS17875 FS36118

Содержимое коробки

Пластиковый литник, Фототравление, Декаль (водная)

Хронология продукта

Новая разработка

Новые детали

Инструкции

Скачать 3306Kb (. pdf)

Магазин

 

Alternative SKUs for Modelcollect UA72201:
MC-UA72201

Заметка: Цены и наличие являются ориентировочными. Также проверьте, действительно ли продукт соответствует!

Oбзор содержимого коробки

 

External reviews

Реклама

Обзор в коробке

Cybermodeler

Обзор в коробке

Aeroscale

Обзор в коробке

IPMS Deutschland

Обзор в коробке

Modellversium

Обзор

FineScale Modeler

Обзор

modelbuilderinternational

Обзор

Britmodeller.com

Обзор Nigel’s Mustang and Models Обзор Model Builder International

 

Запасы

Список желаний (158 Друзья)

Запасы (107 Друзья)

Начатые (8 Друзья)

Завершённые (7x)

Управляйте своим тайником »

Журналы

Этот продукт представлен в следующих выпусках модельного журнала..

Сопутствующие товары

Detail and Conversion sets

B-2A For Modelcollect kit

Eduard 1:72

BIG72136 2018 | Модельный набор B-2A (for Modelcollect)

Eduard 1:72

SS624 2018 | Новая разработка B-2A Bomb Bay (for Modelcollect)

Eduard 1:72

72663 2018 | Новая разработка B-2A (for Modelcollect)

Eduard 1:72

73624 2018 | Изменены детали

Decals

Northrop B-2A Spirit for Modelcollect kit

Caracal Models 1:72

CD720yy 2022* | Новая разработка Spirits in the Materiel World F-4S, F-22A, F-35B, B-2, F-16C

Wolfpak Decals 1:72

72-058 2012 | Новая разработка Несколько моделей (6)

Masks

B-2A (for Modelcollect)

Eduard 1:72

CX504 2018 | Новая разработка

Nameplates

Metal or paintable plastic nameplate for:

B-2 Spirit

Model Monkey 1:72

np-B2-3 2021 | Новая разработка

Проекты

46 изображения

1:72

15 изображения

1:72

Проект: B-2

1:72

Test fitting on the planned display stand. This is huge!

Галерея

Новостная лента

The newsfeed doesn’t contain any items.

Больше о Northrop B-2 Spirit

Northrop B-2 Spirit

Эта тема относится к категории: Авиация » Реактивные » Northrop B-2 Spirit

Книги

B-2 Spirit

In Action Нет. 1178

James Goodall

2002

Все книги » (10 в целом)

Фотообходы

Зарница / Переключатель D-Link DKVM-4K/B2A/B2B 4-портовый KVM-переключатель с портами VGA и PS/2

Комплект для мини-переключателя KVM на 4 порта DKVM-4K является экономически эффективным решением для домашних пользователей или офиса. Комплект позволяет легко управлять четырьмя различными ПК через одну клавиатуру, мышь и монитор VGA. В комплект входит четырехпортовый переключатель KVM (Keyboard, Video and Mouse, Клавиатура, монитор и мышь) и два набора встроенных кабелей, готовых для подключения к ПК. Функции переключателя очень легко использовать, и он великолепно подходит для дома или небольшого офиса.

Основные характеристики	—
Производитель	D-Link
Модель	DKVM-4K
Тип оборудования	KVM переключатель
Кол-во подключаемых системных блоков	4
Корпус	Пластик
Цвета, использованные в оформлении	Серый
Комплект поставки и опции	—
Комплект поставки	2 комплекта кабелей KVM длиной 1. 8 метра
Особенности корпуса	—
Установка в стойку 19″ переключателя KVM	Нет
Интерфейс, разъемы и выходы	—
Управление	Кнопка на передней панели
Консольные подключения	—
Консольная клавиатура	PS/2
Консольная мышь	PS/2
Видео, консоль	D-Sub 15-pin (м)
Максимальное разрешение, консоль	До 2048 x 1536
Питание	—
Блок питания (Вт)	Питание по шине — не требуется внешний адаптер питания
Прочие характеристики	—
Размеры (ширина x высота x глубина)	27.3 x 21.2 x 7 см
Вес (грамм)	300
Рабочая температура	0 ~ 50°C
Логистика	—
Размеры упаковки	27. 3 x 21.2 x 7 см
Вес брутто (грамм)	1.098 кг
Внешние источники информации	—
Горячая линия производителя	(495) 744-00-99
Сервисный центр производителя	Сервисный центр производителя

Вся информация (включая цены) на этом интернет-сайте носит исключительно информационный характер и ни при каких условиях не является публичной офертой, определяемой положениями Статьи 437 (2) Гражданского кодекса РФ. Компания оставляет за собой право в любое время без специального уведомления вносить изменения, удалять, исправлять, дополнять, либо любым иным способом обновлять информацию, размещенную во всех разделах данного сайта. Для получения подробной информации о стоимости, сроках и условиях поставки просьба обращаться по указанным на сайте телефонам.

Теорема Косинусов и Синусов треугольника. Формулы и примеры

Формулировка и доказательство теоремы косинусов

Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.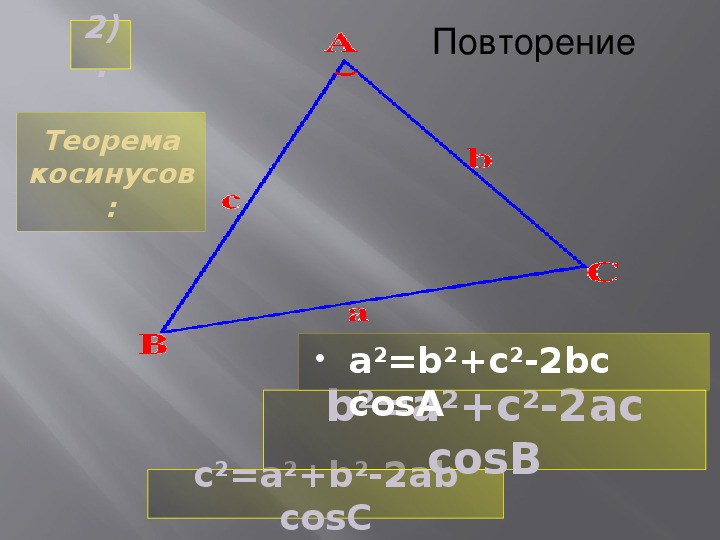

Формула Теоремы Пифагора:

a²> + b²> = c²>, где a, b — катеты, с — гипотенуза.

Из формулы следует: a² = c² — b²

К полученному выражению прибавим и отнимем квадрат второго катета:

Но так как b = c * cos α, то

Эту формулу мы получили для катетов в прямоугольном треугольнике, но аналогичная связь между стороной а и косинусом противолежащего угла справедлива и для произвольного треугольника.

Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Формула теоремы косинусов:

a² = b² + c² — 2bc cos α

В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:

BC² = (x₂ — x₁)² + (y₂ — y₁)²

В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).

BC² = a² = (b cos α — c)² + b²sin²α = b²cos²α + b²sin²α — 2bc cos α + c² = b²(cos²α + sin²α) — 2bc cos α + c²

cos²α + sin²α = 1 — основное тригонометрическое тождество.

b²(cos²α + sin²α) — 2bc cos α + c² = b² + c² — 2bc cos α

Что и требовалось доказать.

Следствие из теоремы косинусов: теорему косинусов также можно использовать для определения косинуса угла треугольника:

 

• Когда b² + c² — a² > 0, угол α будет острым.
• Когда b² + c² — a² = 0, угол α будет прямым.
• Когда b² + c² — a² < 0, угол α будет тупым.

Запоминаем

Когда угол α прямой, то теорема косинусов превращаеся в теорему Пифагора.

Сформулируем еще одно доказательство теоремы косинусов.

Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:

• AD = b * cos α,
• DB = c – b * cos α.

Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:

• h² = b² — (b * cos α)²
• h² = a² — (c – b * cos α)²

Приравниваем правые части уравнений:

• b² — (b * cos α)² = a² — (c — b * cos α)²

либо

• a² = b² + c² — 2bc * cos α

Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.

Определим стороны b и c:

• b² = a² + c² — 2ac * cos β;
• c² = a² + b² — 2ab * cos γ.

Формулировка теоремы для каждой из сторон треугольника

Теорема косинусов справедлива для всех сторон треугольника, то есть:

a² = b² + c² — 2bc cos α

b² = c² + a² — 2ca cos β

c² = a² + b² — 2ab cos γ

Таким образом, теорема косинусов обобщает теорему Пифагора. Закон косинуса может быть использован для любого вида треугольника.

Описание формулы косинуса угла из теоремы косинусов

Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:

Аналогично:

Определение угла с помощью косинуса

А теперь обратим внимание на углы.

Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).

Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.

Рассмотрение пределов изменения cos α и sin α

Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.

Предел изменения косинуса: -1 < cos α < 1.

Предел изменения синуса: 0 < sin α ≤ 1.

• Если cos α > 0, то α ∈ (0°;90°)
• Если cos α < 0, то α ∈ (90°;180°)
• Если cos α = 0, то α = 90°

Примеры решения задач

При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.

Пример 1. Дан треугольник АВС. Найти длину СМ.

∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.

Как решаем:

 

1. Так как АМ + МВ = 9, а AM/MB = 1/2, то АМ = 3, МВ = 6.
   Из треугольника АВС найдем cos B:



2. Из треугольника СМВ по теореме косинусов найдём СМ:
   

Ответ: СМ = √33.

Пример 2. Дан треугольник АВС, в котором a2  + b2 < c2. Доказать, что ∠C — тупой угол.

Как доказываем:

 

1. Для доказательства нужно вспомнить теорему косинусов для угла ∠C: 
   


2. Так как a²  + b² < c², то cos C < 0, следовательно, ∠C — тупой.

Что и требовалось доказать.

Эта задача нам показала, что с помощью теоремы косинусов можно определить тупой угол или острый.

• Если c² = a² + b², то ∠C = 90°.

• Если c² < a² + b², то ∠C — острый.

Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в онлайн-школу Skysmart. Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной.

Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем. Приходите на бесплатный вводный урок математики вместе с ребенком и попробуйте сами!

Формула вершины параболы

☰

Обычно формулу координаты x вершины параболы используют, когда имеют дело с квадратичной функцией.

Квадратичная функция имеет вид: y = ax² + bx + c.

Ее график — это парабола с вершиной, координаты которой определяются по формулам:

Однако формулу координаты y знать и использовать не обязательно. Обычно проще подставить найденное значение x в саму квадратичную функцию и найти оттуда y.

Например, если дана функция y = 2x² – 4x + 5, то координата x ее вершины будет равна:

x = –(–4 / (2 × 2)) = 1

Координату же y вычислим, подставив найденный x в саму функцию:

y = 2 × 12 – 4 × 1 + 5 = 3

Таким образом, вершина графика функции y = 2x² – 4x + 5 находится в точке с координатами (1; 3).

В остальном парабола квадратичной функции вида y = ax

2 + bx + c такая же как функции вида y = ax². Отличие лишь в сдвиге вершины по сравнению с функцией y = ax². Так в приведенном выше примере (y = 2x² – 4x + 5) парабола будет по форме и направлению ветвей такой же, как для функции y = 2x². Разница лишь в координатах вершин парабол.

Формулы вершины параболы получаются при преобразовании квадратичной функции к виду y = f(x + l) + m. Делается это методом выделения полного квадрата. Как известно функции вида y = f(x + l) + m отличаются от функций y = f(x) сдвигом из графиков по оси x на –l и по оси y на m. Именно l в преобразованной квадратичной функции оказывается равным –b/2a, а m = (4ac – b²) / 4a. То есть l и m — это координаты x₀ и y₀ соответственно.

Доказывается это применением метода выделения полного квадрата к квадратному трехчлену общего вида ax² + bx + c. При этом выполняются следующие преобразования:

1. Объединим первые два члена многочлена: y = (ax² + bx) + c

2. Вынесем коэффициент a за скобку, при этом b разделится на a:

3. Представим, что у нас есть квадрат суммы, в котором x одно из слагаемых, а из выражения в скобках надо получить его полный квадрат суммы. Одночлен (b/a)x умножим на 2 и разделим на 2 одновременно. Также прибавим и вычтем квадрат второго слагаемого квадрата суммы. Получим:

4. Выделим квадрат суммы:

5. Умножим на a:

6. Приведем к общему знаменателю свободные члены:

7. Поменяем знак:

Таким образом, мы привели функцию y = ax² + bx + c к виду y = a(x + l)² + m, что соответствует функции y = f(x + l) + m, где f(x) = ax². А как строить графики последней известно.

Новости за 7 дней.

Сколько предметов домашнего обихода должно быть под рукой в ванной комнате? Их десятки. И что с ними делать? Как правило, они не отличаются выдающимся дизайном. Основой набора мебели для ванной комнаты Step стали популярные накладные раковины, устанавливаемые на столешницу, для которых предусмот….

Ассортимент гофрированных труб из нержавеющей стали торговой марки Stahlmann пополнился новыми диаметрами: 40А и 50А. Компания «Электросистемы и технологии» (входит в ГК «ССТ), официальный дистрибьютор бренда Stahlmann, по многочисленным просьбам клиентов расширила ассортимент гибких гофрированны….

Компания группы PORCELANOSA Grupo представляет свои новые коллекции напольного покрытия для наружного применения и самые инновационные технические решения для ванных комнат и систем гидроизоляции в официальных магазинах Испании и Португалии. Butech расширяет свой каталог продукции и технических реш….

В ассортименте EKF появилась эргономичная розетка для кухни со встраиваемой техникой. Новинка c разъёмами типа РШ-ВШ позволяет удобно и эстетично подключить сразу два прибора – варочную панель и духовку. Преимущества нового изделия: привлекательная цена – можно сэкономить до 20 % бюджета; ла….

Серия MPT включает четыре модели носимых видеорегистраторов Dahua со встроенными видеокамерами для ведения аудио- и видеозаписи непосредственно на месте события и формирования в случае происшествия доказательной базы. Эти мобильные устройства предназначены для использования в сфере обеспечения обще….

Одноабонентская вызывная панель IP-видеодомофона VTO2211G-WP обладает элегантным дизайном и тонкой легкой конструкцией. При этом она оснащена всем необходимым для быстрой установки и удобства эксплуатации. Помимо проводного интерфейса Ethernet, который также поддерживает подачу питания PoE, вызывн….

Стремительное развитие технологий и рост современных городов значительно влияют на наш образ жизни, дизайн и архитектуру. В интерьерах стиль лофт лучше всего отражает урбанистический дух, предоставляя простор для творчества и самовыражения. Новая коллекция мебели AQUATON ЛОФТ Урбан объединяет ос….

Решить проблему размещения на плоских кровлях дополнительного оборудования призваны два инновационных технических решения, разработанных Группой компаний fischer, мировым лидером в разработке и производстве современных крепежных изделий. Новые кровельные опоры — FFRB и FFRBH — призваны сделать эксп. 3 \)

Произведение одночлена и многочлена тождественно равно сумме произведений этого одночлена и каждого из членов многочлена.

Этот результат обычно формулируют в виде правила.

Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый из членов многочлена.

Мы уже неоднократно использовали это правило для умножения на сумму.

Произведение многочленов. Преобразование (упрощение) произведения двух многочленов

Вообще, произведение двух многочленов тождественно равно сумме произведении каждого члена одного многочлена и каждого члена другого.

Обычно пользуются следующим правилом.

Чтобы умножить многочлен на многочлен, надо каждый член одного многочлена умножить на каждый член другого и сложить полученные произведения.

Формулы сокращенного умножения. Квадраты суммы, разности и разность квадратов

С некоторыми выражениями в алгебраических преобразованиях приходится иметь дело чаще, чем с другими. 2 = (a — b)(a + b) \) — разность квадратов равна произведению разности на сумму.

Эти три тождества позволяют в преобразованиях заменять свои левые части правыми и обратно — правые части левыми. Самое трудное при этом — увидеть соответствующие выражения и понять, чем в них заменены переменные а и b. Рассмотрим несколько примеров использования формул сокращенного умножения.

Завершение квадрата: получение формулы вершин

Завершение Площадь: Получение формулы вершин (стр. 2 из 2) С вы всегда выполняете одну и ту же процедуру каждый раз, когда находите вершину форма, процедура может быть выполнена символически (используя y = ax 2 + bx + c вместо ввода чисел), так что в итоге вы получите формулу, которую вы можно использовать вместо того, чтобы каждый раз выполнять процесс завершения квадрата. Вот как это выглядит: Вывести формула для координаты x « ч » вершины любой квадратичной. Авторские права © Элизабет Стапель 2000-2011 Все права защищены. Тогда вершина ( h , k ) для любого данное квадратичное y = ax 2 + bx + c подчиняется формуле: Практически говоря, вы можете просто запомнить, что h = — b / (2 a ), а затем подставьте свое значение для « h » вернитесь к « y =», чтобы вычислить « k ».Если вам разрешено использовать эту формулу, вы сможете быстрее найти вершина, потому что простое вычисление h = — b / (2 a ) и затем нахождение k намного быстрее, чем завершение квадрата. С другой стороны, даже если вы не «должны» использовать эту формулу, вы все равно можете использовать это для проверки вашей работы. Если вы не уверены, завершили ли вы квадрат правильно на тесте, вы всегда можете использовать шаблонный ответ, чтобы проверить (или исправьте) все, что вы придумали. Однако если вы запомнили квадратичный Формула, ты можешь вероятно, легко запомнить формулу здесь для k . Дискриминант в квадратичной формуле равен b 2 — 4 ac . Возьми отрицательное значение этого, чтобы получить обратное вычитание: формула для ч имеет знаменатель 2 a ; удвойте это значение, чтобы получить знаменатель 4 a .Сложите их вместе, и вы получите формулу для k . << Предыдущий Наверх | 1 | 2 | Возвращаться в индекс Цитируйте эту статью как: Стапель, Елизавета. «Завершение квадрата: вывод формулы вершины.» Purplemath . Доступен с https://www.purplemath.com/modules/sqrvertx2.htm . Доступ [Дата] [Месяц] 2016 г.

Этот урок можно распечатать для личного пользования.

Упрощение решения или другие простые результаты 5a / b (2a / b2 * 5x / 4a2) Решатель алгебры тигра

Упрощение решения или другие простые результаты 5a / b (2a / b2 * 5x / 4a2) Решатель алгебры тигра

Этот сайт лучший просматривается с помощью Javascript.2 «. Еще 1 похожая замена (и).

Шаг 1:

 x
 Упростить -
            4
 

Уравнение в конце шага 1:

 a a x
  (5 • -) • ((((2 • ————) • 5) • -) • a  2 )
     б (б  2 ) 4
  
 Шаг 2: 
  a
 Упростить ——
            b  2  

Уравнение в конце шага 2:

 a a x
  (5 • -) • ((((2 • ——) • 5) • -) • a  2 )
     б б  2  4
 

Шаг 3:

 
 Умножение экспоненциальных выражений: 
 
 3. 1 a  1 , умноженное на  2  = a  (1 + 2)  = a  3  
 
 Уравнение в конце шага 3: 
  
 a 5a  3  x
  (5 • -) • ————
       b 2b  2  
 Шаг 4: 
 a
 Упростить -
            б
 
 Уравнение в конце шага 4: 
 a 5a  3  x
  (5 • -) • ————
       b 2b  2  
 Шаг 5: 
 
 Умножение экспоненциальных выражений: 
 
 5.1 a  1 , умноженное на a  3  = a  (1 + 3)  = a  4  
 
 Умножение экспоненциальных выражений: 
 
 5,2 b  1  умноженное на b  2  = b  (1 + 2)  = b  3  
 
 Конечный результат: 
  
 25a  4  x
  —————
   2b  3  
 Зачем это изучать 
 Термины и темы 
 Ссылки по теме 
 Формула квадратного уравнения: значение термина -b / 2a 
 Вы, наверное, много раз задавались вопросом, что означает квадратная формула. 2-4 (2) (12)}} {2 (2)} \]  \ [= \ frac {10 \ pm \ sqrt {100-96}} {4} = \ frac {22 \ pm \ sqrt {4}} {4} = \ frac {22 \ pm 2} {4} \]
 что означает, что решениями являются \ (x_1 = 2 \) и \ (x_2 = 3 \).
 Но что означает термин  -b / 2a  в формуле корней квадратного уравнения ?? Очень полезно иметь правильную интуицию по этому поводу.
 Термин -b / 2a имеет четкую графическую интерпретацию и соответствует положению оси симметрии, которое определяется графиком квадратной формулы. Итак, просто член -b / 2a — это «центр» параболы, определяемой квадратным уравнением.
 Вы можете посмотреть видео ниже с хорошим руководством о том, как использовать квадратное уравнение в различных контекстах.
 
 Использовать это 
 программа для решения квадратичных формул 
 показать пошагово вычисление корней квадратного уравнения.
 3.1 — Квадратичные функции 
 3.1 — Квадратичные функции
 Определения 
 Полиномиальная функция от одной переменной степени n
 Функция с одной переменной, возведенной в степень целого числа (наибольшее значение — n) и
с действительными коэффициентами.
 Стандартная форма: f (x) = a  n  x  n  + a  n-1  x  n-1  +. .. + a  2  x  2  + a  1  x + a  0 ,
 а  п  ≠ 0
 Постоянная функция
 Полиномиальная функция от одной переменной степени 0.
 Полиномиальная форма: f (x) = a  0 
 Стандартная форма: f (x) = c
 Линейная функция
 Полиномиальная функция от одной переменной степени 1.
 Полиномиальная форма: f (x) = a  1  x + a  0 
 Стандартная форма: f (x) = ax + b
 Квадратичная функция
 Полиномиальная функция от одной переменной степени 2.
 Полиномиальная форма: f (x) = a  2  x  2  + a  1  x + a  0 
 Стандартная форма 1: f (x) = ax  2  + bx + c
 Стандартная форма 2: f (x) = a (x-h)  2  + k
 Кубическая функция
 Полиномиальная функция от одной переменной степени 3.
 Полиномиальная форма: f (x) = a  3  x  3  + a  2  x  2  + a  1  x + a  0 
 Функция четвертой степени
 Полиномиальная функция от одной переменной степени 4.
 Полиномиальная форма: f (x) = a  4  x  4  + a  3  x  3  + a  2  x  2  + a  1  x + a  0 
 Для степеней выше 4 они обычно обозначаются просто степенью — например, «A»
5 -я полином  степени «
 Парабола
 График квадратичной функции
 Ось симметрии (для параболы)
 Линия симметрии через центр параболы
 Вершина
 Пересечение оси симметрии и параболы.Это будет минимум
точка на графике, если a> 0, и максимальная точка на графике, если a <0.
 Новая «типовая форма» 
 Старая стандартная форма параболы была
записывается как любой другой многочлен, f (x) = ax  2  + bx + c, a 0.
 Мы собираемся завершить квадрат и поместить его в форму, где переводы
 легко интерпретируются. На этот раз вместо разделения на
 вынести a из x-терминов
вместо.
 f (x) = a [x  2  + (b / a) x +? ] + c
 Возьмите половину x-коэффициента и поместите ее на следующую строку.
 f (x) = a [x + (b / 2a)]  2  +?
 Здесь нужно быть осторожным. Когда вы складываете b  2  / (4a  2 ), вы действительно умножаете
это по a, который вы вычленили, так что на самом деле это просто a b  2  / (4a). Этот раз,
 вместо того, чтобы добавлять его к обеим сторонам уравнения, добавьте его и вычтите
 на
та же сторона уравнения.
 f (x) = a [x  2  + (b / a) x + b  2  / (4a  2 )] + c — b  2  / (4a)
 f (x) = a [x + (b / 2a)]  2  + (4ac — b  2 ) / (4a)
 С парой замен это может быть
написано в новой стандартной форме.
 f (x) = a (x — h)  2  + k
, где h = -b / (2a) и k = (4ac — b  2 ) / (4a)
 Не беспокойтесь о том, что такое k, но вы можете
хотите запомнить значение h.
 Координата x вершины -b / (2a). Координата Y — это то, что вы получаете, когда
 вы вставляете -b / (2a) обратно в исходную функцию для x.
 Здесь задействованы три перевода.
 Координаты Y были умножены на  a .Это тот же  и , который был в оригинале.
проблема. Если a> 0, то парабола раскрывается, а вершина находится внизу. Если a <0, то
парабола открывается вниз, а вершина находится наверху.
 Произошел сдвиг по горизонтали. Вместо x-координаты вершины, находящейся в x = 0, это
теперь при x = h, где h = -b / (2a). Поскольку ось симметрии проходит через вершину, то
означает, что ось симметрии теперь x = -b / (2a).
 Произошел вертикальный сдвиг.Координата y вершины теперь равна y = k. Не стоит
самое время запомнить формулу вертикального сдвига. Это не так сложно, это — раз
дискриминант квадратичной, но легче найти координату x и вставить ее обратно в
уравнение для поиска координаты y.
 Если коэффициенты не являются действительно неприятными (например, десятичными), вы можете быстрее заполнить
квадрат, чтобы найти вершину, чем позволить x = -b / (2a), а затем найти координату y.
 Но обратите внимание, что вершина теперь находится в (h, k) вместо (0,0).
 Экстремумы — максимум и минимум 
 Абсолютный минимум
 Если a> 0, то парабола откроется и вершина будет самой низкой точкой на
 график. Так как он ниже всех остальных точек, а не только окружающих
 это, это абсолют
минимум вместо относительного минимума. Поскольку координаты вершины равны
 (h, k),
«абсолютный минимум функции равен k при x = h».
 Абсолютный максимум
 Если a <0, то парабола откроется и вершина будет наивысшей точкой.
 на графике.Поскольку он выше, чем все остальные баллы, а не только те
 вокруг него это абсолют
максимум вместо относительного максимума. Поскольку координаты вершины равны
 (h, k),
«абсолютный максимум функции равен k при x = h».
 Обратите внимание, что правильный формат ответа на минимальный или максимальный вопрос — это дать
минимальное или максимальное значение (координата y)  и , где оно встречается (координата x). 2 $ — Обмен стеками математики
 Сеть обмена стеков 
 Сеть Stack Exchange состоит из 177 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
 Посетить Stack Exchange
 0
 +0
 Авторизоваться
 Зарегистрироваться
 Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях. Регистрация займет всего минуту.
 Зарегистрируйтесь, чтобы присоединиться к этому сообществу
 Кто угодно может задать вопрос
 Кто угодно может ответить
 Лучшие ответы голосуются и поднимаются наверх
 Спросил  4 года, 9 месяцев назад 
 Просмотрено
 3к раз
 $ \ begingroup $
  На этот вопрос уже есть ответы :
 Закрыт 4 года назад. 2 $ для любых $ n \ times n $ матриц?
 Роберт З
 13k1212 золотых знаков8888 серебряных знаков169169 бронзовых знаков
 Создан 03 сен.
 КНгуКНгу
 15711 золотых знаков22 серебряных знака55 бронзовых знаков
 $ \ endgroup $  2  $ \ begingroup $
 В общем случае это неверно, поскольку $ A $ и $ B $ могут не переключаться.2 $$
 
 Создан 03 сен.
 Кармайкл 561
 51. 1k55 золотых знаков5353 серебряных знака9494 бронзовых знака
 $ \ endgroup $  2  Mathematics Stack Exchange лучше всего работает с включенным JavaScript
 Ваша конфиденциальность
 Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в ​​отношении файлов cookie.
 Принимать все файлы cookie 
 Настроить параметры
 Специальные биномиальные произведения 
  Посмотрите, что происходит, когда мы умножаем некоторые двучлены. .. 
 Биномиальное 
 Бином — это многочлен с двумя членами
 пример бинома
 Товар 
  Произведение  означает результат, который мы получаем после умножения.
 В алгебре  xy  означает  x , умноженное на  y 
 И  (a + b) (a − b)  означает  (a + b)   , умноженное на  (a − b) .Мы здесь часто этим пользуемся!
 Специальные биномиальные произведения 
 Итак, когда мы умножаем биномиальные числа, мы получаем … Биномиальные произведения!
 И мы рассмотрим  три частных случая  умножения биномов … так что это  специальных биномиальных произведений .
 1. Умножение бинома на себя 
 Что происходит, когда мы возводим двучлен в квадрат (другими словами, умножаем его на себя) ..?
 (а + б)  2  = (а + б) (а + б) =. ..?
 Результат:
 (a + b)  2  = a  2  + 2ab + b  2 
 На этой иллюстрации показано, почему это работает:
 2. Вычесть, раз Вычесть 
 А что произойдет, если возвести двучлен в квадрат с  минус  внутри?
 (a − b)  2  = (a − b) (a − b) = …?
 Результат:
 (a − b)  2  = a  2  — 2ab + b  2 
 Если вы хотите понять почему, то посмотрите, как квадрат (a − b)  2  равен большому квадрату a  2  за вычетом других прямоугольников:
 
 (a − b)  2  = a  2  — 2b (a − b) — b  2  
 = a  2  — 2ab + 2b  2  — b  2  
 = a  2  — 2ab + b  2 
 3.Сложить раз, вычесть 
 И еще один частный случай … как насчет (a + b) раз (a − b)?
 (a + b) (a − b) = . ..?
 Результат:
 (a + b) (a − b) = a  2  — b  2 
 Это было интересно! Все закончилось очень просто.
 И это называется « разность двух квадратов » (два квадрата:  a  2   и  b  2  ).
 На этой иллюстрации показано, почему это работает:
 a  2  — b  2  равно (a + b) (a − b)
 Примечание: (a − b) может быть первым, а (a + b) вторым:
 (a − b) (a + b) = a  2  — b  2 
 Три дела 
 Вот три результата, которые мы только что получили:
 (а + б)  2 
 = а  2  + 2ab + b  2 
}
 «трехчлены полного квадрата»
 (а-б)  2 
 = a  2  — 2ab + b  2 
 (а + б) (а-б)
 = а  2  — б  2 
 «разница квадратов»
 Запомните эти шаблоны, они сэкономят ваше время и помогут решить множество алгебр.
 Используя их 
 До сих пор мы использовали только «a» и «b», но это могло быть что угодно.
 Пример: (y + 1) 
 2 
 Мы можем использовать случай (a + b)  2 , где «a» — это y, а «b» — 1:
 (y + 1)  2  = (y)  2  + 2 (y) (1) + (1)  2  = y  2  + 2y + 1
 
 Пример: (3x − 4) 
 2 
 Мы можем использовать случай (a-b)  2 , где «a» равно 3x, а «b» — 4:
 (3x − 4)  2  = (3x)  2  — 2 (3x) (4) + (4)  2  = 9x  2  — 24x + 16
 
 Пример: (4y + 2) (4y − 2) 
 Мы знаем, что результат — разница двух квадратов, потому что:
 (a + b) (a − b) = a  2  — b  2 
 так:
 (4y + 2) (4y − 2) = (4y)  2  — (2)  2  = 16y  2  — 4
 Иногда можно увидеть схему ответа:
 Пример: какие двучлены умножаются, чтобы получить 4x 
 2  — 9
 Хммм. 2 $ — MathOverflow
 Сеть обмена стеков 
 Сеть Stack Exchange состоит из 177 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
 Посетить Stack Exchange
 0
 +0
 Авторизоваться
 Зарегистрироваться
 MathOverflow — это сайт вопросов и ответов для профессиональных математиков. Регистрация займет всего минуту.
 Зарегистрируйтесь, чтобы присоединиться к этому сообществу
 Кто угодно может задать вопрос
 Кто угодно может ответить
 Лучшие ответы голосуются и поднимаются наверх
 Спросил  9 лет, 9 мес назад 
 Просмотрено
 10к раз
 $ \ begingroup $  Закрыто. 2 $ и ни $ A $, ни $ B $ не равны нулю.
 
 Создан 18 сен.
 Крис Годсил, Chris Godsil
 11.7k55 золотых знаков3131 серебряный знак5959 бронзовых знаков
 $ \ endgroup $  1 
 MathOverflow лучше всего работает с включенным JavaScript
 Ваша конфиденциальность
 Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в ​​отношении файлов cookie.