Нужно ли сдавать сзв-м если нет сотрудников в организации \ Акты, образцы, формы, договоры \ КонсультантПлюс

• Главная
• Правовые ресурсы
• Подборки материалов
• Нужно ли сдавать сзв-м если нет сотрудников в организации

Подборка наиболее важных документов по запросу Нужно ли сдавать сзв-м если нет сотрудников в организации (нормативно–правовые акты, формы, статьи, консультации экспертов и многое другое).

• Персонифицированный учет:
• 39211620010066000140
• АДИ-5 образец заполнения
• Ади-7
• Выдача сзв-м при увольнении
• Выдача сзв-стаж при увольнении
• Ещё…

• Нулевая отчетность:
• 2-НДФЛ нулевая
• 6-НДФЛ нулевая
• Как заполнить нулевой расчет по страховым взносам
• Нужно ли сдавать нулевую декларацию по УСН
• Нужно ли сдавать нулевую сзв тд
• Ещё…

Зарегистрируйтесь и получите пробный доступ к системе КонсультантПлюс бесплатно на 2 дня

Открыть документ в вашей системе КонсультантПлюс:
Статья: Тест: когда, как и на кого подавать СЗВ-М
(Шаронова Е. А.)
(«Главная книга», 2022, N 9)В форме надо указать данные о лицах, застрахованных по ОПС. В частности, это те, кто работает в организации или у ИП по трудовому договору, выполняет работы или оказывает услуги по гражданско-правовому договору . Если работников и ГПДшников нет, то СЗВ-М сдавать не нужно. Но для организации такое невозможно в принципе, поскольку хотя бы руководитель в ней есть. И на него в отделение ПФР надо подать СЗВ-М .

Зарегистрируйтесь и получите пробный доступ к системе КонсультантПлюс бесплатно на 2 дня

Открыть документ в вашей системе КонсультантПлюс:
Вопрос: Нужно ли сдавать отчет СЗВ-М, если функции единоличного исполнительного органа переданы управляющей организации, а иных работников или лиц, заключивших гражданско-правовые договоры, в обществе нет?
(Консультация эксперта, 2020)Вопрос: Нужно ли сдавать отчет СЗВ-М, если функции единоличного исполнительного органа переданы управляющей организации, а иных работников или лиц, заключивших гражданско-правовые договоры, в обществе нет? Правомерно ли ПФР требует представлять форму СЗВ-М на руководителя управляющей организации?

Зарегистрируйтесь и получите пробный доступ к системе КонсультантПлюс бесплатно на 2 дня

Открыть документ в вашей системе КонсультантПлюс:
Обзор: «Судебные споры зимы 2021 — 2022 года, которые могут заинтересовать бухгалтера»
(КонсультантПлюс, 2022)- АС Поволжского округа признал законным штраф, который получил страхователь за опоздание с СЗВ-М. Работодатель ссылался на то, что сотрудники не представили СНИЛС. Суд указал: страхователь знал о том, что свидетельств нет, и должен был заранее их оформить.

СЗВ-М: если нет работников | Современный предприниматель

Ежемесячная форма СЗВ-М появилась в 2016 году. В 2017 мы продолжаем подавать в Пенсионный фонд сведения о застрахованных лицах на бланке, утвержденном постановлением Правления ПФР от 01.02.2016 № 83п. Изменился лишь срок представления – теперь это 15 число следующего за отчетным месяцем.

Как сдавать СЗВ-М, если нет сотрудников? Как заполнить такую форму? Должен ли отчитываться ИП? Когда не надо подавать сведения? Такие вопросы могут возникать, когда в фирме числится лишь ее руководитель, либо сотрудники еще не набраны, или уже уволены. Мы постараемся ответить на эти вопросы в нашем материале.

Как сдавать СЗВ-М, если нет работников

В отчете СЗВ-М указываются сведения о застрахованных лицах, с которыми в отчетном месяце были заключены, действовали или были расторгнуты трудовые договоры, а также договоры ГПХ, вознаграждения по которым облагаются страховыми пенсионными взносами. Даже если деятельность не ведется, и не уплачиваются взносы, но сотрудники при этом не уволены и договоры с ними действуют, сведения в ПФР подаются.

Логично предположить, что если такие договоры не заключались, то и отчитываться не о чем: СЗВ-М без сотрудников будет пустой. Но в любой организации всегда есть ее руководитель, который одновременно является ее сотрудником, а значит, одного застрахованного в сведениях, в большинстве случаев, все же следует указать.

Вновь созданные и неработающие фирмы: СЗВ-М без работников

Как правило, у фирм, зарегистрированных не так давно, деятельность еще не ведется, а штат сотрудников поначалу отсутствует. Также возможна ситуация, когда работающая организация приостанавливает на неопределенный срок свою хоздеятельность и увольняет всех работников. Как сдавать СЗВ-М, если нет сотрудников по таким причинам?

Здесь следует обратить внимание на то, как оформлены трудовые отношения с директором организации:

• Если директор в новой фирме пока не назначен, а есть только учредители, то СЗВ-М не подается. Когда директора приняли на работу, подписав с ним трудовой договор, включать в сведения для ПФР его нужно с месяца заключения договора.
• Приостанавливая деятельность, организация перестанет заполнять отчет СЗВ-М, если нет сотрудников, со следующего месяца после расторжения последнего договора, по которому отчислялись страхвзносы ПФР. Если же деятельности нет, но договоры не расторгнуты, например, в связи с уходом сотрудников в отпуск без содержания, то придется по-прежнему подавать сведения СЗВ-М.

Как сдать СЗВ-М, если нет работников, а директор – учредитель

• С директором заключен трудовой договор и он получает зарплату, облагаемую пенсионными взносами – в этом случае СЗВ-М, если нет работников, нужно сдать на одного директора-учредителя (письмо ПФР от 13.07.2016 № ЛЧ-08-26/9856).
• Трудовой договор не заключался, хоздеятельность организацией не ведется и зарплата директору не выплачивается – сведения СЗВ-М при таких обстоятельствах сдавать не нужно (Информация с сайта ПФР о порядке представления формы СЗВ-М).

СЗВ-М для ИП без работников

Пока предприниматель использует труд наемных работников, он является страхователем в ПФР и обязан ежемесячно отчитываться по форме СЗВ-М. Причем, в сведениях ИП должен указывать только своих сотрудников, но не себя.

А когда ИП без работников сдает СЗВ-М? Ответ на этот вопрос один – никогда. Если предприниматель всегда работал в одиночку или все его работники по трудовым и ГПХ-договорам уволены, и поэтому наемных сотрудников в отчетном месяце у него нет, представлять СЗВ-М ему не нужно вовсе (письмо ПФР от 27.07.2016 № ЛЧ-08-19/10581).

Как заполнить СЗВ-М, если нет работников

Если заключенных, действующих, или расторгнутых в отчетном месяце трудовых договоров и договоров ГПХ у страхователя нет, то и заполнять форму СЗВ-М не нужно.

Заполнять СЗВ-М при отсутствии работников придется фактически лишь в случае, когда в организации работает по трудовому договору только ее директор. В разделе 4 нужно заполнить лишь одну строку, указав сведения о застрахованном лице – директоре. Он же подписывает сведения СЗВ-М за отчетный месяц в качестве руководителя.

Все, что вам нужно знать о машинах опорных векторов

Машина опорных векторов (SVM) определяется как алгоритм машинного обучения, который использует модели обучения с учителем для решения сложных задач классификации, регрессии и обнаружения выбросов путем выполнения оптимальных преобразований данных, которые определять границы между точками данных на основе предопределенных классов, меток или выходных данных. В этой статье объясняются основы SVM, их работа, типы и несколько реальных примеров.

Содержание

• Что такое метод опорных векторов?
• Как работает машина опорных векторов?
• Типы машин опорных векторов
• Примеры машин опорных векторов

Что такое метод опорных векторов?

Машина опорных векторов (SVM) — это алгоритм машинного обучения, который использует модели обучения с учителем для решения сложных задач классификации, регрессии и обнаружения выбросов путем выполнения оптимальных преобразований данных, которые определяют границы между точками данных на основе предварительно определенных классов, меток или выходы. SVM широко используются в таких областях, как здравоохранение, обработка естественного языка, приложения для обработки сигналов и области распознавания речи и изображений.

Технически основная цель алгоритма SVM состоит в том, чтобы идентифицировать гиперплоскость, которая четко разделяет точки данных разных классов. Гиперплоскость локализована таким образом, что наибольший запас разделяет рассматриваемые классы.

Представление опорного вектора показано на рисунке ниже:

SVM оптимизируют границу между опорными векторами или классами

гиперплоскость без каких-либо внутренних опорных векторов. Такие гиперплоскости легче определить для линейно разделимых задач; однако для реальных задач или сценариев алгоритм SVM пытается максимизировать разницу между опорными векторами, тем самым приводя к неправильным классификациям для меньших участков точек данных.

SVM потенциально предназначены для решения задач двоичной классификации. Однако с ростом количества многоклассовых задач, требующих больших вычислительных ресурсов, создается несколько бинарных классификаторов, которые объединяются для формулировки SVM, которые могут реализовывать такие многоклассовые классификации с помощью двоичных средств.

В математическом контексте SVM относится к набору алгоритмов машинного обучения, которые используют методы ядра для преобразования характеристик данных с помощью функций ядра. Функции ядра основаны на процессе сопоставления сложных наборов данных с более высокими измерениями таким образом, чтобы упростить разделение точек данных. Функция упрощает границы данных для нелинейных задач, добавляя более высокие измерения для отображения сложных точек данных.

При введении дополнительных измерений данные не полностью преобразуются, поскольку они могут действовать как вычислительный процесс. Этот метод обычно называют уловкой ядра, при котором преобразование данных в более высокие измерения достигается эффективно и недорого.

Идея алгоритма SVM была впервые сформулирована в 1963 году Владимиром Н. Вапником и Алексеем Я. Червоненкис. С тех пор SVM приобрели достаточную популярность, поскольку они продолжают иметь широкомасштабное применение в нескольких областях, включая процесс сортировки белков, категоризацию текста, распознавание лиц, автономные автомобили, роботизированные системы и так далее.

Узнать больше: Что такое нейронная сеть? Определение, работа, типы и приложения в 2022 году

Как работает машина опорных векторов?

Работу машины опорных векторов можно лучше понять на примере. Предположим, у нас есть красные и черные метки с функциями, обозначенными x и y. Мы намерены иметь классификатор для этих тегов, который классифицирует данные либо по красной, либо по черной категории.

Давайте нанесем размеченные данные на плоскость x-y, как показано ниже:

Типичный SVM разделяет эти точки данных на красные и черные теги с помощью гиперплоскости, которая в данном случае является двумерной линией. Гиперплоскость обозначает линию границы решения, в которой точки данных попадают под красную или черную категорию.

Гиперплоскость определяется как линия, которая расширяет поля между двумя ближайшими тегами или метками (красной и черной). Расстояние от гиперплоскости до ближайшей метки является наибольшим, что упрощает классификацию данных.

Приведенный выше сценарий применим к линейно разделимым данным. Однако для нелинейных данных простая прямая линия не может разделить отдельные точки данных.

Вот пример нелинейного сложного набора данных:

Приведенный выше набор данных показывает, что одной гиперплоскости недостаточно для разделения задействованных меток или тегов. Однако здесь векторы явно различаются, что облегчает их разделение.

Для классификации данных необходимо добавить еще одно измерение в пространство признаков. Для линейных данных, обсуждавшихся до этого момента, было достаточно двух измерений x и y. В этом случае мы добавляем z-размер, чтобы лучше классифицировать точки данных. Более того, для удобства воспользуемся уравнением для окружности z = x² + y².

С третьим измерением срез пространства признаков вдоль направления z выглядит следующим образом:

Теперь, с тремя измерениями, в этом случае гиперплоскость проходит параллельно направлению x при определенном значении z; давайте рассмотрим это как z = 1.

Остальные точки данных дополнительно сопоставляются с двумя измерениями.

На приведенном выше рисунке показана граница для точек данных вдоль объектов x, y и z вдоль окружности окружности с радиусом 1 единица, которая разделяет две метки тегов через SVM.

Давайте рассмотрим другой метод визуализации точек данных в трех измерениях для разделения двух тегов (в данном случае двух теннисных мячей разного цвета). Рассмотрим шары, лежащие на двумерной плоской поверхности. Теперь, если мы поднимем поверхность вверх, все теннисные мячи будут распределены в воздухе. Два шара разного цвета могут разделиться в воздухе в какой-то момент этого процесса.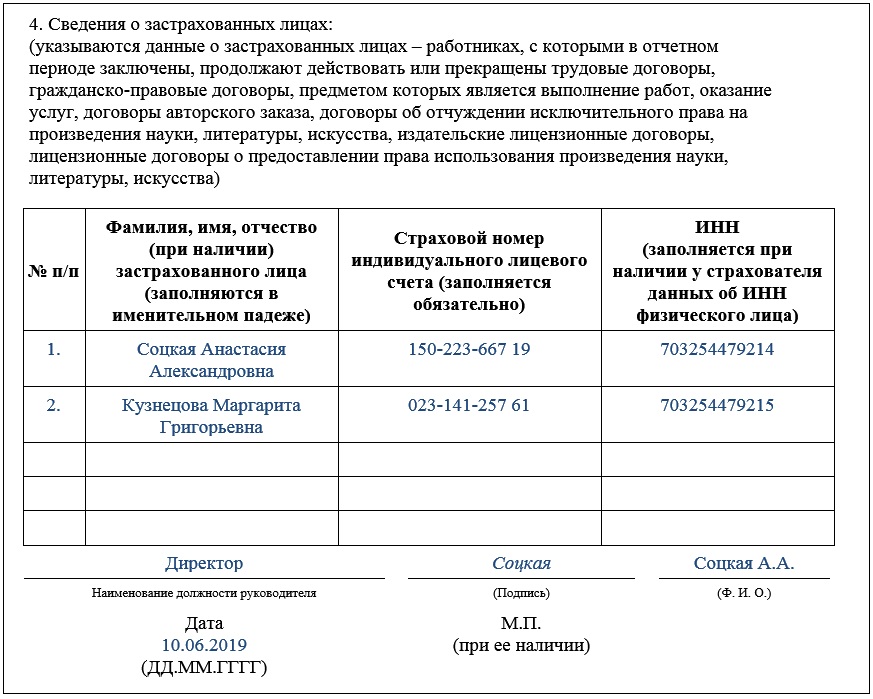 Пока это происходит, вы можете использовать или поместить поверхность между двумя отдельными наборами шариков.

Во всем этом процессе акт «подъема» 2D-поверхности относится к событию отображения данных в более высокие измерения, что технически называется «кернеллингом», как упоминалось ранее. Таким образом, сложные точки данных могут быть разделены с помощью большего количества измерений. Подчеркнутая здесь концепция заключается в том, что точки данных продолжают отображаться в более высоких измерениях до тех пор, пока не будет идентифицирована гиперплоскость, которая показывает четкое разделение между точками данных.

На рисунке ниже представлена ​​трехмерная визуализация описанного выше варианта использования:

Подробнее: Узкий ИИ, общий ИИ и супер-ИИ: ключевые сравнения

Типы машин опорных векторов

можно разделить на два типа: простой или линейный SVM и ядерный или нелинейный SVM.

1. Простой или линейный SVM

Линейный SVM относится к типу SVM, используемому для классификации линейно разделимых данных. Это означает, что когда набор данных можно разделить на категории или классы с помощью одной прямой линии, он называется линейным SVM, а данные называются линейно различными или разделимыми. Более того, классификатор, который классифицирует такие данные, называется линейным классификатором SVM.

Простой SVM обычно используется для решения задач классификации и регрессионного анализа.

2. Ядро или нелинейный SVM

Нелинейные данные, которые нельзя разделить на отдельные категории с помощью прямой линии, классифицируются с использованием ядра или нелинейного SVM. Здесь классификатор называется нелинейным классификатором. Классификацию можно выполнять с нелинейным типом данных, добавляя признаки в более высокие измерения, а не полагаясь на двумерное пространство. Здесь недавно добавленные функции соответствуют гиперплоскости, которая помогает легко разделять классы или категории.

SVM ядра обычно используются для решения задач оптимизации с несколькими переменными.

Подробнее : Что такое анализ настроений? Определение, инструменты и приложения

Примеры машин опорных векторов

SVM полагаются на контролируемые методы обучения для классификации неизвестных данных по известным категориям. Они находят применение в различных областях.

Здесь мы рассмотрим некоторые из лучших реальных примеров SVM:

1. Решение проблемы геозондирования

Проблема геозондирования — один из широко распространенных вариантов использования SVM, в котором процесс используется для отслеживания слоистой структуры планеты. Это влечет за собой решение проблем инверсии, когда наблюдения или результаты проблем используются для факторизации переменных или параметров, которые их произвели.

При этом линейная функция и алгоритмические модели опорных векторов разделяют электромагнитные данные. Кроме того, в этом случае при разработке моделей с учителем используются методы линейного программирования. Поскольку размер задачи значительно мал, размер измерения неизбежно будет крошечным, что объясняет картографирование структуры планеты.

2. Оценка потенциала сейсмического разжижения

Разжижение грунта является серьезной проблемой, когда происходят такие события, как землетрясения. Оценка его потенциала имеет решающее значение при проектировании любой гражданской инфраструктуры. SVM играют ключевую роль в определении появления и отсутствия таких аспектов разжижения. Технически SVM выполняют два теста: SPT (стандартное испытание на проникновение) и CPT (испытание на конусное проникновение), которые используют полевые данные для оценки сейсмического статуса.

Кроме того, SVM используются для разработки моделей, включающих несколько переменных, таких как факторы грунта и параметры разжижения, для определения прочности поверхности грунта. Считается, что SVM достигают точности, близкой к 96-97% для таких приложений.

3. Дистанционное обнаружение гомологии белков

Дистанционная гомология белков — это область вычислительной биологии, в которой белки классифицируются по структурным и функциональным параметрам в зависимости от последовательности аминокислот, когда идентификация последовательности кажется затруднительной. SVM играют ключевую роль в удаленной гомологии, при этом функции ядра определяют общность между белковыми последовательностями.

Таким образом, SVM играют определяющую роль в вычислительной биологии.

4. Классификация данных

Известно, что SVM решают сложные математические задачи. Однако сглаженные SVM предпочтительнее для целей классификации данных, в которых используются методы сглаживания, которые уменьшают выбросы данных и делают шаблон идентифицируемым.

Таким образом, для задач оптимизации гладкие SVM используют алгоритмы, такие как алгоритм Ньютона-Армиджо, для обработки больших наборов данных, которые не могут использовать обычные SVM. Гладкие типы SVM обычно используют математические свойства, такие как сильная выпуклость, для более простой классификации данных, даже с нелинейными данными.

5. Обнаружение лиц и классификация выражений

SVM классифицируют лицевые структуры по сравнению с другими. В обучающих данных используются два класса объекта лица (обозначается +1) и объекта без лица (обозначается -1) и n * n пикселей, чтобы различать структуры лица и не лица. Далее анализируется каждый пиксель, и из каждого извлекаются признаки, обозначающие лицевые и нелицевые символы. Наконец, процесс создает квадратную границу решения вокруг лицевых структур на основе интенсивности пикселей и классифицирует полученные изображения.

Кроме того, SVM также используются для классификации выражений лица, которая включает выражения, обозначаемые как счастливые, грустные, сердитые, удивленные и так далее.

6. Классификация текстуры поверхности

В текущем сценарии SVM используются для классификации изображений поверхностей. Подразумевается, что изображения поверхностей, на которые нажимают, могут быть переданы в SVM для определения текстуры поверхностей на этих изображениях и классификации их как гладких или шероховатых поверхностей.

7. Категоризация текста и распознавание рукописного ввода

Категоризация текста относится к классификации данных по предопределенным категориям. Например, новостные статьи содержат информацию о политике, бизнесе, фондовом рынке или спорте. Точно так же можно разделить электронные письма на спам, не спам, нежелательную почту и другие.

Технически каждой статье или документу присваивается оценка, которая затем сравнивается с предопределенным пороговым значением. Статья классифицируется в соответствующую категорию в зависимости от оцененного балла.

Для примеров распознавания рукописного ввода набор данных, содержащий отрывки, написанные разными людьми, передается в SVM. Как правило, классификаторы SVM сначала обучаются на выборочных данных, а затем используются для классификации почерка на основе значений баллов. Впоследствии SVM также используются для разделения текстов, написанных людьми и компьютерами.

8. Распознавание речи

В примерах распознавания речи слова из речи выбираются и разделяются по отдельности. Далее для каждого слова извлекаются определенные признаки и характеристики. Методы извлечения признаков включают кепстральные коэффициенты частоты Mel (MFCC), коэффициенты линейного предсказания (LPC), кепстральные коэффициенты линейного предсказания (LPCC) и другие.

Эти методы собирают аудиоданные, передают их в SVM, а затем обучают модели распознаванию речи.

9. Обнаружение стенографии

С помощью SVM вы можете определить, является ли какое-либо цифровое изображение искаженным, загрязненным или чистым. Такие примеры полезны при решении вопросов, связанных с безопасностью, для организаций или государственных учреждений, поскольку проще шифровать и вставлять данные в качестве водяного знака в изображения с высоким разрешением.

Такие изображения содержат больше пикселей; следовательно, может быть сложно обнаружить скрытые сообщения или сообщения с водяными знаками. Однако одним из решений является разделение каждого пикселя и сохранение данных в разных наборах данных, которые впоследствии могут быть проанализированы SVM.

10. Обнаружение рака

Медицинские работники, исследователи и ученые во всем мире усердно трудятся над поиском решения, позволяющего эффективно обнаруживать рак на ранних стадиях. Сегодня для этого используется несколько инструментов AI и ML. Например, в январе 2020 года Google разработала инструмент искусственного интеллекта, который помогает в раннем выявлении рака молочной железы и снижает количество ложных срабатываний и отрицательных результатов.

В таких примерах можно использовать SVM, в которых раковые изображения могут подаваться в качестве входных данных. Алгоритмы SVM могут анализировать их, обучать модели и, в конечном итоге, классифицировать изображения, которые выявляют признаки злокачественного или доброкачественного рака.

Подробнее : Что такое дерево решений? Алгоритмы, шаблоны, примеры и лучшие практики

Выводы

SVM имеют решающее значение при разработке приложений, включающих реализацию прогностических моделей. SVM легко понять и развернуть. Они предлагают сложный алгоритм машинного обучения для обработки линейных и нелинейных данных через ядра.

SVM находят применение в каждой области и в реальных сценариях, где данные обрабатываются путем добавления пространств более высоких измерений. Это влечет за собой рассмотрение таких факторов, как настройка гиперпараметров, выбор ядра для выполнения и вложение времени и ресурсов в фазу обучения, что помогает разрабатывать модели обучения под наблюдением.

Помогла ли вам эта статья понять концепцию машин опорных векторов? Комментарий ниже или сообщите нам о Facebook , Twitter , или LinkedIn . Мы хотели бы услышать от вас!

• Что такое аналитика данных? Определение, типы и приложения
• Что такое квантовые вычисления? Работа, важность и использование
• Что такое HCI (взаимодействие человека с компьютером)? Значение, важность, примеры и цели
• Что такое язык программирования COBOL? Определение, примеры, использование и проблемы
• Что такое Кортана? Определение, работа, функции и проблемы

Машинный классификатор опорных векторов в Python; Прогнозирование вероятности текучести кадров с помощью Itertools и Gridsearch | Рой Поланитцер

Машина опорных векторов — это модель обучения с учителем, которая, как k ближайших соседей, деревья решений, случайный лес и повышение градиента, может использоваться для прогнозирования непрерывной переменной, а также для классификации категориальной переменной. Классификатор опорных векторов использует линейную функцию значений признаков, чтобы разделить наблюдения на две категории: 1 (да, отток и т. д.) или 0 (нет, остаться и т. д.). Другими словами, модель классификатора машины опорных векторов предсказывает P(Y=1) как функцию X.

• Метод опорных векторов пытается классифицировать наблюдения, определяя путь, разделяющий классы.
• В простейшей ситуации уравнение для каждой стороны пути представляет собой линейную функцию признаков, и все наблюдения классифицируются правильно. Это называется жестким разделением.
• Идеальное разделение обычно невозможно, и существует компромисс между шириной пути и нарушениями.
• Для наблюдения, расположенного не на правильной стороне пути, степень нарушения измеряется кратчайшим расстоянием между наблюдением и местом, где оно было бы правильно классифицировано.
• Работая с функциями значений признаков, а не с самими значениями признаков, путь, разделяющий наблюдения на два класса, можно сделать нелинейным. Можно создавать новые функции, которые являются квадратами, кубами, четвертыми степенями и т. Д. Из значений функций.

Помня об этом выше, давайте посмотрим на наш набор данных.

Набор данных получен от Kaggle и связан с сотрудниками крупной телекоммуникационной компании. Цель классификации состоит в том, чтобы предсказать, покинет ли работник фирму (1) или нет (0) (переменная y). Набор данных можно скачать отсюда.

 импортировать pandas как pd 
 импортировать numpy как np 
 из sklearn импортировать предварительную обработку 
 импортировать matplotlib.pyplot как plt 
 plt.rc («шрифт», размер = 14) 
 из sklearn.linear_model импортировать LogisticRegression 
 из sklearn.test_split импорт train_test_selection 
 импортировать Seaborn как sns 
 sns.set(style=”white”) 
 sns.
  set(style=”whitegrid”, color_codes=True) 

Набор данных предоставляет информацию о сотрудниках компании. Он включает 14 999 записей и 10 полей.

 data = pd.read_csv('HR_comma_sep.csv') 
 data = data.dropna() 
 print(data.shape) 
 print(list(data.columns)) 

(14999, 10)
[ ‘satisfaction_level’, ‘last_evaluation’, ‘number_project’, ‘average_montly_hours’, ‘time_spend_company’, ‘Work_accident’, ‘promotion_last_5years’, ‘department’, ‘salary’, ‘y’]

 data.head() 

Входные переменные

1. уровень удовлетворенности : уровень удовлетворенности сотрудника (числовой)
2. last_evaluation : время с момента последней оценки в годах (числовое)
3. number_projects : количество проектов, выполненных за время работы (числовое: 2, 3, 4, 5, 6, 7) )
4. time_spend_company : время, проведенное в компании в годах (числовые: 2, 3, 4, 5, 6, 7, 8, 10)
5. Work_accident : имел ли сотрудник несчастный случай на рабочем месте (категория: «1» , «0»)
6. Promotion_last_5years : был ли сотрудник повышен в должности за последние пять лет (категория: «1», «0»)
7. отдел: отдел, в котором работает сотрудник (категория: «продажи», «бухгалтерский учет», «управление персоналом», «технический», «поддержка», «управление»,
   «ИТ», «управление продуктами», «маркетинг». “, “RandD“)
8. оклад : относительный уровень заработной платы (категория: «низкая», «средняя», «высокая»)

Прогнозируемая переменная (желаемая цель): Компания? (бинарный: «1» означает «Да», «0» означает «Нет»)

Столбец отдела в наборе данных имеет много категорий, и нам нужно уменьшить категории для лучшего моделирования. Столбец отдела имеет следующие категории:

 data['department'].unique() 

 data['department']=np.where(data['department'] =='support', 'technical', data['department']) 
 data['department']=np.where(data[ 'отдел'] == 'ИТ', 'технический', данные ['отдел']) 
 data['department'].unique() 

 data['y']. value_counts() 

 sns.countplot(x='y', данные=данные, палитра='hls') 
 plt.show() 
 plt .savefig('count_plot') 

 count_no_churn = len(data[data['y']==0]) 
 count_churn = len(data[data['y']==1]) 
  pct_of_no_churn = count_no_churn/( count_no_churn+count_churn) 
 print("\033[1m процент оттока не равен", pct_of_no_churn*100) 
 pct_of_churn = count_churn/(count_no_churn+count_churn) 
 print("\033[1m процент оттока", pct_of_churn*100) 

 data.groupby('y').mean() 

 data.groupby('отдел').mean() 

 data.groupby('Work_accident').mean() 

 data.groupby('promotion_last_5years').mean() 

 %matplotlib встроенный 
 data.satisfaction_level.hist() 
 plt.title('Гистограмма уровня удовлетворенности') 
 plt.xlabel('satisfaction_level') 
 plt .ylabel('Frequency') 
 plt.savefig('hist_satisfaction_level') 

 data.last_evaluation.hist() 
 plt.title('Гистограмма последней оценки') 
 plt.xlabel('last_evaluation') 
 plt.ylabel(‘Frequency’) 
 plt.savefig(‘hist_last_evaluation’) 

 table=pd. crosstab(data.number_project,data.y) 
 table.div(table.sum(1).astype(float), axis=0).plot(kind='bar', stacked=True) 
 plt.title('Гистограмма количества проектов по сравнению с оттоком') 
 plt.xlabel('Количество проектов') 
 plt.ylabel('Доля сотрудников') 
 plt.savefig('number_project_vs_churn_stack') 

 data.average_montly_hours.hist() 
 plt.title('Гистограмма среднего количества часов за месяц') 
 plt.xlabel('average_montly_hours') 
 plt.ylabel('Частота') 
 plt.savefig('hist_average_montly_hours') 
 
 Большинство сотрудников компании в этом наборе данных имеют medium_montly_hours в диапазоне 150–200. 
 
 table=pd.crosstab(data.Work_accident,data.y) 
 table.div(table.sum(1).astype(float), axis=0).plot(kind='bar', stacked=True) 
 plt.title('Гистограмма с накоплением несчастных случаев на работе и оттока') 
 plt.xlabel('Work_accident') 
 plt. ylabel('Доля сотрудников') 
 plt.savefig('Work_accident_vs_churn_stack') 
 Work_accident кажется хороший предиктор переменной результата.
 table=pd.crosstab(data.time_spend_company,data.y) 
 table.div(table.sum(1).astype(float), axis=0).plot(kind='bar', stacked=True) 
 plt.title('Гистограмма с накоплением времени, проведенного в компании по сравнению с оттоком') 
 plt.xlabel('Время, проведенное в компании') 
 plt.ylabel('Доля сотрудников') 
 plt.savefig('time_spend_company_vs_churn_stack') 
 Time_spend_company кажется сильным предиктором переменной результата.
 table=pd.crosstab(data.promotion_last_5years,data.y) 
 table.div(table.sum(1).astype(float), axis=0).plot(kind='bar', stacked=True) 
 plt.title('Гистограмма повышения по службе за последние 5 лет по сравнению с оттоком') 
 plt.xlabel('Повышение по службе за последние 5 лет') 
 plt.ylabel('Доля сотрудников') 
 plt.savefig('promotion_last_5years_vs_churn_stack') 
 Promotion_last_5years может быть хорошим предиктором результата.
 table=pd.crosstab(data.department,data.y) 
 table.div(table.sum(1).astype(float), axis=0).plot(kind='bar', stacked=True) 
 plt.title('Гистограмма с накоплением отдела по сравнению с оттоком') 
 plt.xlabel('отдел') 
 plt.ylabel('Доля сотрудников') 
 plt.savefig('department_vs_churn_stack') 
 Департамент, кажется, быть хорошим предиктором переменной результата.
 table=pd.crosstab(data.salary,data.y) 
 table.div(table.sum(1).astype(float), axis=0).plot(kind='bar', stacked=True) 
 plt.title('Гистограмма с накоплением зарплат и оттока') 
 plt.xlabel('salary') 
 plt.ylabel('Доля сотрудников') 
 plt.savefig('salary_vs_churn_stack') 
 Заработная плата, по-видимому, является хорошим предиктором переменной результата.
 Это переменные только с двумя значениями, нулем и единицей.
 cat_vars=['Work_accident','time_spend_company','promotion_last_5years','department','salary'] 
 для var в cat_vars: 
 cat_list='var'+'_'+var 
 cat_list = pd. get_dummies(data[var], prefix=var) 
 data1=data.join(cat_list) 
 data=data1cat_vars=[' Work_accident','time_spend_company','promotion_last_5years','department','salary'] 
 data_vars=data.columns.values.tolist() 
 to_keep=[i for i в data_vars, если я не в cat_vars] 
 Наш финал столбцы данных будут:
 data_final=data[to_keep] 
 data_final.columns.values ​​
   array(['satisfaction_level', 'last_evaluation', 'number_project', 
 'average_montly_hours', 'y', 'Work_accident_0', 'Work_accident_1', 
 'time_spend_company_2', 'time_spend_company_3', 
 'time_spend_company_4', 'time_spend_company_5', 
 'time_spend_company_6', 'time_spend_company_7', 
 'time_spend_company_8', ' time_spend_company_10', 
 'promotion_last_5years_0', 'promotion_last_5years_1', 
 'department_RandD', 'department_accounting', 'department_hr', 
 'department_management', 'department_marketing', 
 'department',s'product_dmng0264 'department_technical', 'salary_high', 'salary_low', 
 'salary_medium'], dtype=object)  
 Создав обучающие данные, я передискретизирую класс оттока, используя алгоритм SMOTE (Synthetic Minority Oversampling). Техника). На высоком уровне SMOTE:
 Работает путем создания синтетических семплов из второстепенного класса (т. е. класса churn) вместо создания копий.
 Случайный выбор одного из k ближайших соседей и использование его для создания подобных, но случайно измененных новых наблюдений.
 Мы собираемся реализовать SMOTE на Python.
 X = data_final.loc[:, data_final.columns != 'y'] 
 y = data_final.loc[:, data_final.columns == 'y'] from imblearn.over_sampling import SMOTEos = SMOTE(random_state=42) 
 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0,33, random_state=42) 
 столбца = X_train.columnsos_data_X,os_data_y=os.fit_sample(X_train, y_train) 
 os_data_X = pd.DataFrame(data=os_data_X ,columns=columns ) 
 os_data_y= pd.DataFrame(data=os_data_y,columns=['y'])# мы можем проверить номера наших данных 
 print("\033[1m Длина передискретизированных данных ",len(os_data_X)) 
 print("\033[1m Число неизменяемых данных передискретизируемых",len(os_data_y[os_data_y['y']==0 ])) 
 print("\033[1m Число оттока",len(os_data_y[os_data_y['y']==1])) 
 print("\033[1m Доля данных без оттока в передискретизированных данных " ,len(os_data_y[os_data_y['y']==0])/len(os_data_X)) 
 print("\033[1m Доля оттока данных в передискретизированных данных ",len(os_data_y[os_data_y['y'] ==1])/len(os_data_X)) 
   ДЛИНА ДАННЫХ ПЕРЕВАНИЯ БОЛЬШЕ - 15318  
   Количество NO DACURN в данных о перевышенной дискретике 7659  
   Количество churn 7659  9007 34. S. 9028. 9028. 9028. 9028. 9028.
   Доля данных об оттоке в данных передискретизации составляет 0,5  
 Теперь у нас есть идеально сбалансированные данные! Вы, возможно, заметили, что я передискретизировал только обучающие данные, потому что при передискретизации только обучающих данных никакая информация в тестовых данных не используется для создания синтетических наблюдений, поэтому никакая информация не будет просачиваться из тестовых данных в обучение модели.
 Itertools — это модуль в python, он используется для перебора структур данных, которые можно пройти с помощью цикла for. Такие структуры данных также известны как итерируемые. Этот модуль включает в себя функции, которые эффективно используют вычислительные ресурсы. комбинации() предоставляет нам все возможные кортежи, последовательность или набор чисел или букв, используемых в итераторе, и элементы считаются уникальными на основе их позиций, которые различны для всех элементов.
 import itertoolssl = itertools. combinations([1,2,3,4],3) 
 for i in l: 
 print(i) 
   (1, 2, 3) 
 (1, 2, 4) 
 (1, 3, 4) 
 (2, 3, 4)  
 os_data_X.columns 
   Index(['satisfaction_level', 'last_evaluation', 'number_hoursac_montly_project', '
 , 'Work_accident_1', 
 'time_spend_company_2', 'time_spend_company_3', 'time_spend_company_4', 
 'time_spend_company_5', 'time_spend_company_6', 'time_spend_company_7', 
 'time_spend_company_8', 'time_spend_company_10', 
 'romotion_last_5years_0', 'ramotion_last_5years_1', 
 'Department_randd', 'Department_ACCOUNTING', Department_, Department_M.M. Department_technical ', 
' зарплата_high ',' arleary_low ',' зарплата_медия '], 
 dtype =' obj ) 
 os_data_y1 = os_data_y.copy()os_data_X1.rename(columns={'satisfaction_level': "A", 'last_evaluation': "B", 'number_project': "C", 'average_montly_hours': "D", 'Work_accident_0' : "E", 'Work_accident_1': "F", 'time_spend_company_2': "G", 'time_spend_company_3': "H", 'time_spend_company_4': "I", 'time_spend_company_5': "J", 'time_spend_company_6': " K", 'time_spend_company_7': "L", 'time_spend_company_8': "M", 'time_spend_company_10': "N", 'promotion_last_5years_0': "O", 'promotion_last_5years_1': "P", 'department_RandD': "Q" , 'department_accounting': "R", 'department_hr': "S", 'department_management': "T", 'department_marketing': "U", 'department_product_mng': "V", 'department_sales': "W", ' Department_technical': "X", 'salary_high': "Y", 
 'salary_low': "Z", 'salary_medium': "a"}, inplace=True)os_data_X1. columns 

 os_data_y1.rename(columns={'y': «Цель»}, inplace=True) 
 os_data_y1.columns 

 из sklearn.svm импортировать SVC 
 из sklearn.metrics import precision_score 
 из sklearn.metrics import f1_scorefor i in range(1,28): 
 c = itertools.combinations("ABCDEFGHIJKLMNOPQRSTUVWXYZa",i) 
 для элемента в c: 
 ls = list(item) 
 X_train, X_test, y_train, y_test = train_test_split(os_data_X1[ls], os_data_y1['Target'], test_size= 0,33,random_state=42) 
 модель = SVC() 
 model.fit(X_train,y_train) 
 y_pred = model. predict(X_train) 
 y_pred1 = model.predict(X_test) 
 accuarcy = показатель точности (y_train, y_pred) 
 accuarcy1 = показатель точности (y_test, y_pred1) 
 # print(ls,accuarcy) 
, если точность1: > 0,90 
 print(ls," Точность на тренировочном наборе: {:.4%}".format(accuarcy), " Точность на тестовом наборе: {:.4%}".format(accuarcy1)) 
 

 Cols = ['Last_evaluation', 'number_project', 'time_spend_company_2', 'time_spend_scompane_3 '3'. 
 из sklearn.svm импортировать SVC 
 из sklearn импортировать метрики 
 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42) 
 svc = SVC() 
 svc.fit(X_train, y_train) y_pred = svc.predict(X_test) 
 print('Точность машинного классификатора опорных векторов в тестовом наборе: {:. 2f}'.format(svc.score(X_test, y_test))) 
   Точность машинного классификатора опорных векторов на тестовом наборе: 0,92  
 Gridsearch — это метод настройки, который пытается вычислить оптимальные значения гиперпараметров. Это исчерпывающий поиск, который выполняется по конкретным значениям гиперпараметров модели. Модель также известна как оценочная. Поиск по сетке может сэкономить нам время, усилия и ресурсы. Gridsearch — простейший алгоритм настройки гиперпараметров. По сути, мы делим область гиперпараметров на дискретную сетку. Затем мы пробуем каждую комбинацию значений этой сетки, вычисляя некоторые показатели производительности с помощью перекрестной проверки.
 Во-первых, давайте импортируем GridsearchCV из SciKit Learn.
 из sklearn.model_selection import GridSearchCV 
 Затем давайте создадим словарь с именем param_grid и заполним некоторые параметры для C и гаммы.
 param_grid  =  {'C' : [0. 01, 0.1, 1, 10, 100], 'gamma': [0.01, 0.1, 1, 10, 100] } 
 После этого давайте создадим объект GridSearchCV и подгоним это к обучающим данным.
 grid = GridSearchCV(SVC(), param_grid, refit=True, verbose=2) 
 grid.fit(X_train, y_train) 
 Теперь давайте выясним, какие гиперпараметры модели являются лучшими модель.
 svc = SVC(C=100, gamma=100, вероятность=True) 
 svc.fit(X_train, y_train) 
   SVC(C=100, gamma=100, вероятность=True)  
7 Прогнозирование результатов набора тестов и расчет точности 
 y_pred = svc.predict(X_test) 
 print('Точность машинного классификатора опорных векторов на тестовом наборе: {:.2f}'.format(svc.score(X_test, y_test))) 
   Точность машинного классификатора опорных векторов на тестовом наборе: 0,93  
 из sklearn.metrics импорта путаницы_матрицы 
 svm_cm = metrics.confusion_matrix(y_pred, y_test, [1,0]) 
 sns. heatmap(svm_cm, annot=True, fmt='.2f',xticklabels = ["Churn", "No-Churn"] , yticklabels = ["Churn", "No-Churn"] ) 
 plt.ylabel('Истинный класс') 
 plt.xlabel('Прогнозируемый класс') 
 plt.title('Классификатор опорных векторов') 
 plt.savefig('Support_Vector_Machine_Classifier') 
 Результат говорит нам, что у нас есть   2325+2378   правильных прогнозов и  5 неправильных прогнозов  146+2 .
 Цитата из Scikit Learn:
 Точность — это отношение tp / (tp + fp), где tp — количество истинных срабатываний, а fp — количество ложных срабатываний. Точность — это интуитивно способность классификатора не маркировать образец как положительный, если он отрицательный.
 Отзыв — это отношение tp / (tp + fn), где tp — количество истинных положительных результатов, а fn — количество ложноотрицательных результатов. Под отзывом понимается интуитивно способность классификатора находить все положительные образцы.
 Показатель F-бета можно интерпретировать как средневзвешенное гармоническое значение точности и отзыва, где показатель F-бета достигает своего наилучшего значения при 1, а наихудший показатель при 0.
 Показатель F-бета взвешивает отзыв больше чем точность коэффициентом бета. бета = 1,0 означает, что полнота и точность одинаково важны.
 Поддержка — это количество вхождений каждого класса в y_test.
 из sklearn.metrics importclassification_report 
 print(classification_report(y_test, y_pred)) 
 Когда сотрудник увольняется, как часто мой классификатор предсказывает это правильно? Это измерение называется «отзывом». Из всех случаев оборота классификатор машины опорных векторов распознал 2378 случаев оборота (TP-истинно положительный) из 2524 случаев оборота (TP=2378 и FN=146) во всем наборе тестов. Это означает оборот «отзыва» около 94% (2378/2524).
 Когда классификатор предсказывает увольнение сотрудника, как часто этот сотрудник фактически увольняется? Это измерение называется «точность». Классификатор машины опорных векторов правильно предсказал 2378 случаев (TP) как случаи оборота из 2584 случаев (TP = 2378 и FP = 206) во всем наборе тестов. Это означает «точность» оборота около 92% (2378/2584).
 из sklearn.metrics import roc_auc_score 
 из sklearn.metrics import roc_curve 
 svc_roc_auc = roc_auc_score(y_test, svc.predict(X_test)) 
 fpr, tpr, thresholds = roc_curve(y_test, svc.predict_proba(X_test)[:,1]) 
 plt.figure() 
 plt.plot(fpr, tpr, label='SVC (площадь = %0.2f)' % svc_roc_auc) 
 plt.plot([0, 1], [0, 1],'r — ') 
 plt.xlim([0,0, 1,0]) 
 plt.ylim([0,0, 1,05]) 
 plt. xlabel('Коэффициент ложных срабатываний') 
 plt.ylabel('Коэффициент истинных срабатываний') 
 plt.title('Рабочая характеристика приемника') 
 plt.legend(loc="нижний правый") 
 plt.savefig('svc_ROC' ) 
 plt.show() 
 Кривая рабочих характеристик приемника (ROC) — еще один распространенный инструмент, используемый с бинарными классификаторами. Пунктирная линия представляет ROC-кривую чисто случайного классификатора; хороший классификатор остается как можно дальше от этой линии (по направлению к верхнему левому углу).
 Записная книжка Jupyter, использованная для создания этого поста, доступна здесь. Буду рад получить отзывы или вопросы по любому из вышеперечисленных.
 Теперь я собираюсь распечатать список сотрудников, которые, по прогнозам модели, могут быть уволены.
 df = X_test.copy() 
 df['True'] = y_test 
 df['Predicted'] = y_pred 
 prob = svc.predict_proba(X_test)[:,1] 
 df['вероятность'] = prob 
 df1 = pd.concat([df['Истина'], df['Прогноз'], df['вероятность']], axis=1) 
 df1.columns = [‘истина’, ‘прогноз’, ‘вероятность’] 
 df1 
 Машина опорных векторов — это контролируемый алгоритм машинного обучения, который можно использовать как для задач классификации, так и для регрессии. Тем не менее, он в основном используется в задачах классификации.
 В этом алгоритме мы отображаем каждый элемент данных как точку в n-мерном пространстве (где n — количество имеющихся у вас объектов), где значение каждого объекта является значением конкретной координаты.