Как рассчитывается годовая процентная ставка: Как начисляются проценты по кредиту? | КонсультантПлюс
Функция СТАВКА — Служба поддержки Office
В этой статье описаны синтаксис формулы и использование функции СТАВКА в Microsoft Excel.
Описание
Возвращает процентную ставку за один период аннуитета. Ставка вычисляется путем итерации и может иметь ноль или более решений. Если последовательные результаты ставка не сходятся с в пределах 0,0000001 после 20 итерации, то ставка возвращает результат #NUM! значение ошибки #ЗНАЧ!.
Синтаксис
СТАВКА(кпер; плт; пс; [бс]; [тип]; [прогноз])
Примечание: Полное описание аргументов «кпер», «плт», «пс», «бс» и «тип» см.
Аргументы функции СТАВКА описаны ниже.
-
Кпер — обязательный аргумент. Общее количество периодов платежей по аннуитету.
-
Плт Обязательный. Выплата, производимая в каждый период и не меняющаяся на протяжении всего периода ежегодного платежа. Обычно аргумент «плт» состоит из основного платежа и платежа по процентам, но не включает других налогов и сборов. Если он опущен, аргумент «пс» является обязательным.
-
Пс — обязательный аргумент. Стоимость на данный момент — общая сумма, которая на данный момент оценивается в ряду будущих платежей.

-
Пс Необязательный. Будущая стоимость, или величина остатка средств, которая нужна после последней выплаты. Если пс опущен, предполагается значение 0 (например, будущая стоимость для займа — 0). Если аргумент «пс» опущен, аргумент «пс» является обязательным.
-
Тип Необязательный. Число 0 или 1, обозначающее, когда должна производиться выплата.
Тип | Когда нужно платить |
|---|---|
|
0 или опущен |
В конце периода |
|
1 |
В начале периода |
Замечания
Убедитесь, что единицы измерения, выбранные для аргументов «прогноз» и «кол_пер» соответствуют друг другу. При ежемесячных выплатах по четырехгодичному займу под 12 процентов годовых используйте значение 12%/12 для аргумента «прогноз» и 4*12 — для аргумента «кол_пер». При ежегодных платежах по тому же займу используйте значение 12% для аргумента «прогноз» и 4 —для аргумента «кол_пер».
При ежемесячных выплатах по четырехгодичному займу под 12 процентов годовых используйте значение 12%/12 для аргумента «прогноз» и 4*12 — для аргумента «кол_пер». При ежегодных платежах по тому же займу используйте значение 12% для аргумента «прогноз» и 4 —для аргумента «кол_пер».
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Данные | Описание | |
|---|---|---|
|
4 |
Срок займа в годах |
|
-200 |
Ежемесячная сумма платежа |
|
|
8000 |
Сумма займа |
|
|
Формула |
Описание |
Результат |
|
=СТАВКА(A2*12; A3; A4) |
Месячная процентная ставка по займу в соответствии с условиями, указанными в диапазоне A2:A4 в качестве аргументов. |
1 % |
|
=СТАВКА(A2*12; A3; A4)*12 |
Годовая процентная ставка по займу в соответствии с теми же условиями. |
9,24 % |
Как работают процентные ставки? | справочный центр dYdX
Краткий обзорНа платформе действуют «плавающие» процентные ставки. Это значит, что они постоянно меняются в зависимости от спроса. Это также значит, что ставка не фиксируется во время открытия позиции и может измениться за время, пока позиция остается открытой.
Для каждого актива существует ставка по займу и ставка кредитования. Ставки колеблются в зависимости от коэффициента утилизации — это соотношение средств, взятых в кредит, и средств, которые кредиторы готовы выдать в долг. С ростом коэффициента утилизации процентная ставка будет расти, что привлечет на рынок дополнительных кредиторов. При снижении коэффициента утилизации процентная ставка будет падать.
С ростом коэффициента утилизации процентная ставка будет расти, что привлечет на рынок дополнительных кредиторов. При снижении коэффициента утилизации процентная ставка будет падать.
Процент выплачивается непрерывно. Это означает, что вы можете закрыть позицию или вывести средства в любое время, не беспокоясь о сроке блокирования средств. Это также означает, что процент постоянно капитализируется. Все ставки приведены в годовом исчислении (APR) (годовая ставка с учетом капитализации (APY) выше).
Как рассчитывается процентная ставка?
Процентная ставка для заемщиковНа платформе действуют плавающие процентные ставки, которые рассчитываются исходя из текущего коэффициента утилизации на рынке. Коэффициент утилизации — это соотношение средств, взятых в кредит, и средств, которые кредиторы готовы выдать в долг, на конкретном рынке. 64) = 5.00% APR
64) = 5.00% APR
Таким образом, годовая процентная ставка для заемщиков растет нелинейно от 0 % до 50 %.
Процентная ставка для кредиторовС математической точки зрения ставка кредитования должна быть не выше ставки по займу, потому что процентные платежи не берутся из ниоткуда. При этом 5 % от общей суммы полученных на платформе процентных платежей отчисляются в страховой фонд, который защищает протокол в периоды избыточной волатильности. Поскольку процентная ставка по займу применяется пропорционально ко всем выданным в кредит средствам, то ставка кредитования рассчитывается так (B — ставка заимствования):
95% * (B * X)Поскольку на все залоговое обеспечение в dYdX непрерывно начисляется процент, не исключено, что ваше обеспечение приносит вам больший процентный доход, чем вы выплачиваете по займу. В таком случае на вкладке «Маржа» на странице «Торговля» будет показана отрицательная процентная ставка к уплате.
Показанная процентная ставка — это текущая процентная ставка, которую вы ожидаете выплатить по своим заемным средствам. Поскольку ваше залоговое обеспечение приносит процентный доход (а суммы обеспечения могут быть разными в зависимости от вашего кредитного плеча), то изменение кредитного плеча позиции перед ее открытием может изменить показанную процентную ставку.
Страница не найдена — RES$A
RESSA GLOBAL LTD 2018/
2018/ Предупреждение о риске: Ressa Global не несет никакой ответственности за утрату ваших денег в результате того, что вы положились на информацию, содержащуюся на этом сайте, включая данные, котировки, графики сигналы , рекомендации менеджера. Вся информация которая публикуется либо доносится клиенту несет в себе рекомендационный характер . Компания Ressa analytics не является участником биржевой торговли, форекс брокером. Компания Ressa Global получает прибыль за счет выставленных тарифов за предоставления рекомендационной информации и обучения клиентов. С какой брокерской организацией вести биржевую деятельность клиент решает самостоятельно. Учитывайте высочайший уровень риска, связанный с инвестированием в финансовые рынки.Торговля или инвестиции на бирже связаны с потенциальными рисками. Цены на рынках чрезвычайно волатильны и могут изменяться под действием разнообразных финансовых новостей, законодательных решений или политических событий. Торговля на биржах подходит не всем инвесторам. Прежде чем начать торговать на международной бирже или любом другом финансовом инструменте, включая криптовалюты, вы должны правильно оценить цели инвестирования, уровень своей экспертизы и допустимый уровень риска. Спекулируйте только теми деньгами, которые Вы можете позволить себе потерять.
С какой брокерской организацией вести биржевую деятельность клиент решает самостоятельно. Учитывайте высочайший уровень риска, связанный с инвестированием в финансовые рынки.Торговля или инвестиции на бирже связаны с потенциальными рисками. Цены на рынках чрезвычайно волатильны и могут изменяться под действием разнообразных финансовых новостей, законодательных решений или политических событий. Торговля на биржах подходит не всем инвесторам. Прежде чем начать торговать на международной бирже или любом другом финансовом инструменте, включая криптовалюты, вы должны правильно оценить цели инвестирования, уровень своей экспертизы и допустимый уровень риска. Спекулируйте только теми деньгами, которые Вы можете позволить себе потерять.
Ressa Global напоминает вам, что данные, предоставленные на данном сайте, не обязательно даны в режиме реального времени и могут не являться точными. Все цены на акции, индексы, фьючерсы и криптовалюты носят ориентировочный характер и на них нельзя полагаться при торговле. Таким образом, Ressa Global Ltd не несет никакой ответственности за любые убытки, которые вы можете понести в результате использования этих данных.
Таким образом, Ressa Global Ltd не несет никакой ответственности за любые убытки, которые вы можете понести в результате использования этих данных.
Ressa Global может получать компенсацию от рекламодателей, упоминаемых на страницах издания, основываясь на вашем взаимодействии с рекламой или рекламодателями.
. All Rights Reserved.
CFA — Как вычислять эффективную годовую процентную ставку (EAR)? | программа CFA
Рассмотрим порядок расчета эффективной годовой процентной ставки (EAR) на основе заявленной годовой ставки и периодичности начисления процентов, а также примеры применения EAR в финансовых вычислениях.
Банки и финансовые организации обычно котируют ставки своих продуктов как заявленные годовые процентные ставки (англ. ‘stated annual interest rate’). Эта ставка является суммой периодических ставок, по которым начисляются проценты в течение года.
Например, банк будет указывать своим клиентам проценты по вкладу с поквартальным начислением как 8% за год (т. е. 2% * 4), а не как периодическую ставку 2% за квартал.
е. 2% * 4), а не как периодическую ставку 2% за квартал.
Ставка процента, которую инвесторы получат фактически, называется эффективной годовой процентной ставкой (EAR, от англ. ‘effective annual rate’).
EAR представляет собой годовую норму прибыли, фактически полученную после начисления всех процентов в промежуточные периоды.
Формулу EAR может представить следующим образом:
EAR = (1 + Периодическая процентная ставка) m — 1,
где:
- Периодическая процентная ставка (англ. ‘periodic interest rate’) = Заявленная годовая ставка / m;
- m = Количество периодов начисления за год.
Очевидно, что EAR для заявленной ставки в 8% при годовом начислении не совпадает с EAR для ставки 8% при полугодовом или ежеквартальном начислении.
Действительно, при использовании сложных процентов, заявленная годовая ставка и фактическая (эффективная) годовая процентная ставка равны только тогда, когда проценты начисляются ежегодно.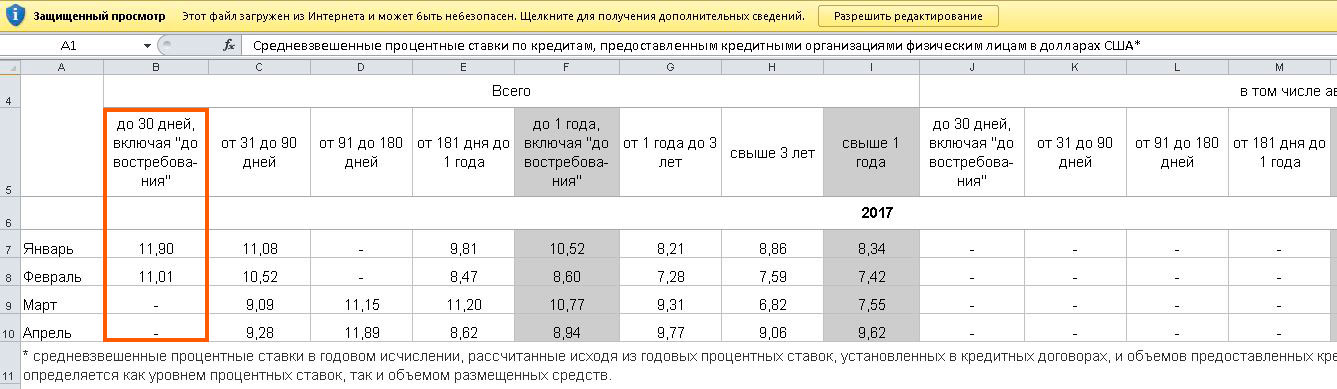
В противном случае, чем больше частота или периодичность начисления процентов (англ. ‘compounding frequency’), тем сумма процентов по EAR будет больше суммы процентов по заявленной процентной ставке.
Расчет ставки EAR необходим при сравнении инвестиций с разными периодами начисления процентов. Образно говоря, EAR позволяет сравнивать яблоки с грушами.
Пример расчета ставки EAR.
Необходимо вычислить EAR, если заявленная годовая ставка составляет 12%, с ежеквартальным начислением процентов.
Решение.
Здесь m = 4, поэтому периодическая ставка составляет 12/4 = 3%.
Таким образом,
EAR = (1 + 0.03)4 — 1 = 1.1255 — 1 = 0.1255 = 12.55%.
Для расчета этого выражения на финансовом калькуляторе используйте клавишу [yx].
Порядок нажатия клавиш на калькуляторе TI для вышеупомянутого вычисления будет: 1,03 [yx] 4 [=].
Пример вычисления ставки EAR с разной периодичностью начисления процентов.

Используя заявленную ставку 6%, вычислите EAR при полугодовом, ежеквартальном, ежемесячном и ежедневном начислении процентов.
Решение.
EAR при полугодовом начислении процентов =
(1 + 0.03)2 — 1 = 1.06090 — 1 = 0.06090 = 6.090%.
EAR при квартальном начислении процентов =
(1 + 0.015)4 — 1 = 1.06136 — 1 = 0.06136 =6.136%.
EAR при ежемесячном начислении процентов =
(1 + 0.005) 12 — 1 = 1.06168 — 1 = 0.06168 = 6.168%.
EAR при ежедневном начислении процентов =
(1 + 0.00016438)365 — 1 = 1.06183 — 1 = 0.06183 = 6.183%.
Обратите внимание на то, что EAR увеличивается с увеличением периодичности начисления.
Примеры использования эффективной ставки процента в финансовых вычислениях с промежуточными периодами.
Когда промежуточные периоды отличаются от годовых, мы должны учитывать этот факт в наших расчетах. Рассмотрим следующие два примера.
Рассмотрим следующие два примера.
Пример роста инвестиций с ежеквартальным начислением процентов.
Джон планирует инвестировать $2 500 на счет, который будет приносить 8% годовых с ежеквартальным начислением.
Сколько денег будет на счете через два года?
Решение.
В данном примере имеется 8 квартальных периодов начисления за 2 года, а эффективная ежеквартальная ставка EAR составляет:
8% / 4 = 2%.
Рост суммы инвестиций составит:
2 500 * (1.02)8 = $ 2 929.15.
Можно сделать альтернативный расчет, рассчитав сначала годовую ставку EAR:
Годовая ставка EAR составляет:
1,024 — 1 = 0,082432.
Теперь мы можем вычислить рост $2 500 по годовой эффективной ставке 8.2432% за два года:
2 500 * (1.082432)2 = $2 929.15,
что является тем же результатом.
Пример определения текущей стоимости инвестиций с ежемесячным начислением процентов.

Алиса хотела бы, чтобы ее банковский вклад на счете вырос до $5 000 за 3 года. Если заявленная доходность вклада составляет 9% годовых с ежемесячным начислением процентов, то какой должна быть сумма первоначального вклада, чтобы Алиса достигла своей финансовой цели через 3 года?
Решение.
Эффективная месячная ставка составляет:
9% / 12 = 0,75%.
Первоначальная сумма вклада, обеспечивающая рост до $5 000 через 3 года (36 месяцев) составляет:
5 000 / (1.0075)36 = $3 820,74.
В качестве альтернативы можно сначала рассчитать годовую ставку EAR:
1.007512 — 1 = 0,093807.
Теперь можно рассчитать первоначальную (т.е. текущую или приведенную) стоимость, дисконтируя $5 000 по годовой ставке EAR:
5,000 / 1.0938073 = $3,820.74,
что дает тот же результат.
Эффективная годовая ставка (EAR) — Как рассчитать эффективную процентную ставку
Что такое эффективная годовая процентная ставка?
Эффективная годовая процентная ставка (EAR) — это процентная ставка, скорректированная для начисления сложных темпов роста Совокупный темп роста — это показатель, специально используемый в контексте бизнеса и инвестирования, который указывает темпы роста за несколько периодов времени. Это показатель постоянного роста ряда данных. Самым большим преимуществом совокупной скорости роста является то, что метрика учитывает эффект сложения.за определенный период. Проще говоря, эффективная годовая процентная ставка — это процентная ставка. Процентные расходы. Процентные расходы возникают из-за компании, которая финансирует за счет заемных средств или аренды капитала. Процентная ставка указывается в отчете о прибылях и убытках, но также может указываться, что инвестор может заработать (или заплатить) через год после учета сложного процента.
Это показатель постоянного роста ряда данных. Самым большим преимуществом совокупной скорости роста является то, что метрика учитывает эффект сложения.за определенный период. Проще говоря, эффективная годовая процентная ставка — это процентная ставка. Процентные расходы. Процентные расходы возникают из-за компании, которая финансирует за счет заемных средств или аренды капитала. Процентная ставка указывается в отчете о прибылях и убытках, но также может указываться, что инвестор может заработать (или заплатить) через год после учета сложного процента.
EAR можно использовать для оценки процентов, подлежащих уплате по ссуде или долгу, или для оценки доходов от инвестиций, таких как гарантированный инвестиционный сертификат (GIC) или сберегательный счет.
Эффективная годовая процентная ставка также известна как эффективная процентная ставка (EIR), годовая эквивалентная ставка (AER) или эффективная ставка. Сравните это с годовой процентной ставкой (APR). Годовая процентная ставка (APR) Годовая процентная ставка (APR) — это годовая процентная ставка, которую физическое лицо должно платить по ссуде или которую они получают на депозитный счет. В конечном итоге, годовая процентная ставка — это простой процентный термин, используемый для выражения числовой суммы, ежегодно выплачиваемой физическим или юридическим лицом за право заимствования денег.который основан на простом интересеПростой интересПростой процентной формуле, определении и примере. Простой процент — это расчет процентов, который не учитывает эффект начисления процентов. Во многих случаях проценты складываются с каждым назначенным периодом ссуды, но в случае простых процентов это не так. Расчет простых процентов равен основной сумме, умноженной на процентную ставку, умноженной на количество периодов.
Годовая процентная ставка (APR) Годовая процентная ставка (APR) — это годовая процентная ставка, которую физическое лицо должно платить по ссуде или которую они получают на депозитный счет. В конечном итоге, годовая процентная ставка — это простой процентный термин, используемый для выражения числовой суммы, ежегодно выплачиваемой физическим или юридическим лицом за право заимствования денег.который основан на простом интересеПростой интересПростой процентной формуле, определении и примере. Простой процент — это расчет процентов, который не учитывает эффект начисления процентов. Во многих случаях проценты складываются с каждым назначенным периодом ссуды, но в случае простых процентов это не так. Расчет простых процентов равен основной сумме, умноженной на процентную ставку, умноженной на количество периодов.
Формула EAR приведена ниже:
Где:
- i = Заявленная годовая процентная ставка ставка
- n = Количество периодов начисления сложных процентов
Эффективная годовая ставка на основе начисления процентов
В таблице ниже показана разница в эффективной годовой ставке при изменении периодов начисления сложных процентов.
Таблица: Курс CFI по основам фиксированного дохода
Например, EAR заявленной процентной ставки 1%, начисляемой ежеквартально, составляет 1,0038%.
Важность эффективной годовой ставки
Эффективная годовая процентная ставка — важный инструмент, позволяющий оценить истинную доходность инвестиций или истинную процентную ставку по ссуде.
Заявленная годовая процентная ставка и эффективная процентная ставка могут значительно отличаться из-за начисления сложных процентов.Эффективная процентная ставка важна для определения наилучшего кредита или определения того, какие инвестиции предлагают самую высокую норму доходности. Внутренняя норма доходности (IRR) Внутренняя норма доходности (IRR) — это ставка дисконтирования, которая составляет чистую приведенную стоимость (NPV). ) нулевого проекта. Другими словами, это ожидаемая совокупная годовая норма прибыли, которая будет получена от проекта или инвестиций.
В случае начисления сложных процентов EAR всегда выше установленной годовой процентной ставки.
EAR Пример
Например, предположим, что банк предлагает вашему депозиту в размере 10 000 долларов США установленную процентную ставку 12%, начисляемую ежемесячно.В таблице ниже представлена концепция эффективной годовой процентной ставки:
Таблица: Курс CFI по основам фиксированного дохода
Процентная ставка за 1 месяц: начальный баланс (10 000 долларов) x процентная ставка (12% / 12 = 1% ) = 100 долларов США
Процентная ставка за месяц 2: Начальный баланс (10 100 долларов США) x процентная ставка (12% / 12 = 1%) = 101 доллар США
Изменение в процентах от начального баланса (10000 долларов США) до конечного баланса ( 11 268 долларов) равно (11 268 — 10 000 долларов) / 10 000 =.12683 или 12,683%, что является эффективной годовой процентной ставкой. Несмотря на то, что банк предлагал заявленную процентную ставку 12%, ваши деньги выросли на 12,683% за счет ежемесячного начисления сложных процентов.
Эффективная годовая процентная ставка позволяет определить истинную рентабельность инвестиций (ROI) Формула ROI (Return on Investment) Рентабельность инвестиций (ROI) — это финансовый коэффициент, используемый для расчета выгоды, которую инвестор получит по отношению к своим инвестициям. Стоимость. Чаще всего он измеряется как чистая прибыль, деленная на первоначальные капитальные затраты на инвестиции.Чем выше коэффициент, тем больше полученная выгода.
Скачать бесплатный шаблон
Введите свое имя и адрес электронной почты в форму ниже и загрузите бесплатный шаблон, показанный выше!
Как рассчитать эффективную процентную ставку?
Чтобы рассчитать эффективную процентную ставку по формуле EAR, выполните следующие действия:
1. Определите заявленную процентную ставку
Заявленная процентная ставка (также называемая годовой процентной ставкой или номинальной ставкой) обычно находится в заголовки договора займа или депозита. Пример: «Годовая ставка 36%, проценты взимаются ежемесячно».
Пример: «Годовая ставка 36%, проценты взимаются ежемесячно».
2. Определите количество периодов начисления сложных процентов
Периоды начисления сложных процентов обычно бывают ежемесячными или ежеквартальными. Периоды начисления сложных процентов могут составлять 12 (12 месяцев в году) и 4 квартальных (4 квартала в году).
Для справки:
- Ежемесячно = 12 периодов начисления начислений
- Квартально = 4 периода начисления начислений
- Двухнедельные = 26 периодов начисления начислений
- Еженедельно = 52 периода начисления начислений
- Ежедневно = 365 периодов начисления начислений
3 .Примените формулу EAR: EAR = (1+ i / n)
n — 1Где:
- i = заявленная процентная ставка
- n = периоды начисления процентов
Пример
Для расчета эффективной годовой процентной ставки по кредитной карте с годовой ставкой 36% и ежемесячным начислением процентов:
1. Заявленная процентная ставка: 36%
Заявленная процентная ставка: 36%
2. Количество периодов начисления сложных процентов: 12
Таким образом, EAR = (1 + 0.12 — 1 = 0,4257 или 42,57%.
Почему банки не используют эффективную годовую процентную ставку?
Когда банки взимают проценты, вместо эффективной годовой процентной ставки используется указанная процентная ставка. Это делается для того, чтобы потребители поверили, что они платят более низкую процентную ставку.
Например, для ссуды с установленной процентной ставкой 30%, начисляемой ежемесячно, эффективная годовая процентная ставка будет 34,48%. Банки обычно рекламируют заявленную процентную ставку 30%, а не эффективную процентную ставку 34.48%.
Когда банки выплачивают проценты по вашему депозитному счету, EAR объявляется более привлекательным, чем заявленная процентная ставка.
Например, для депозита с установленной ставкой 10% ежемесячно, эффективная годовая процентная ставка будет 10,47%. Банки будут рекламировать эффективную годовую процентную ставку 10,47%, а не заявленную процентную ставку в 10%.
По сути, они показывают ту ставку, которая кажется более выгодной.
Дополнительная литература
CFI — глобальный поставщик курсов финансового моделирования и сертификации финансовых аналитиков. Станьте сертифицированным аналитиком финансового моделирования и оценки (FMVA) ®.Чтобы продолжить карьеру финансового профессионала, ознакомьтесь со следующими дополнительными ресурсами CFI:
- Ожидаемая доходность Ожидаемая доходность Ожидаемая доходность инвестиций — это ожидаемая величина распределения вероятностей возможной прибыли, которую они могут предоставить инвесторам. Доходность инвестиций — это неизвестная переменная, у которой разные значения, связанные с разными вероятностями.
- Базовые точки Базисные точки (BPS) Базовые точки (BPS) — это обычно используемая метрика для измерения изменений процентных ставок.Базовая точка — одна сотая процента. См. Примеры. Этот показатель
- Прирост капитала Доходность Прирост капитала Доходность Доходность прироста капитала (CGY) — это удорожание инвестиции или ценной бумаги, выраженное в процентах.
 Поскольку расчет доходности прироста капитала включает рыночную цену ценной бумаги с течением времени, его можно использовать для анализа колебаний рыночной цены ценной бумаги. См. Расчет и пример
Поскольку расчет доходности прироста капитала включает рыночную цену ценной бумаги с течением времени, его можно использовать для анализа колебаний рыночной цены ценной бумаги. См. Расчет и пример - Средневзвешенная стоимость капитала (WACC) WACCWACC — это средневзвешенная стоимость капитала компании, которая представляет собой смешанную стоимость капитала, включая собственный капитал и заемные средства.
Как рассчитывается процент по кредитной карте (APR)?
Когда дело доходит до основ кредитных карт, наиболее важным понятием является то, как начисляются проценты. Большинство эмитентов карт рассчитывают процентные платежи, используя «средний дневной остаток», что означает, что ваши проценты рассчитываются ежедневно. Поняв, как часто рассчитываются ваши проценты, вы сможете определить, сколько вы должны.
Даже если вы не рассчитываете вручную проценты по кредитной карте, все равно важно понимать, как эмитенты определяют ваши проценты.В конце мы добавили наш собственный калькулятор процентов, чтобы упростить вам этот процесс. Это руководство поможет вам четко понять каждый этап расчета и предоставит ключевые термины, которые вам следует знать.
Это руководство поможет вам четко понять каждый этап расчета и предоставит ключевые термины, которые вам следует знать.
Как работают проценты по кредитной карте?
Проценты по кредитной карте применяются к вашей выписке, если вы не выплатите остаток в полном объеме к дате платежа. Чтобы узнать свою процентную ставку, вы захотите посмотреть годовую процентную ставку (APR) на вашей карте. Вероятно, будут разные годовые ставки в зависимости от транзакции, такой как покупки, переводы баланса и авансы наличными.Годовая процентная ставка за покупку является наиболее распространенной процентной ставкой, и, как следует из названия, годовая процентная ставка за покупку взимается с товаров, которые вы покупаете на своей карте.
Как рассчитать проценты по кредитной карте, шаг за шагом
Расчет процентов по кредитной карте может быть сложным процессом. Расчет состоит из четырех этапов, и определение среднего дневного баланса будет самым сложным из них. Это требует, чтобы вы точно знали, каким был ваш баланс в конце каждого дня в течение последнего платежного цикла.
Шаг 1. Выясните, как часто начисляются проценты по вашей кредитной карте
Первый шаг — выяснить, как часто начисляются проценты по вашей кредитной карте — как часто проценты добавляются к вашему первоначальному балансу. Большинство эмитентов кредитных карт ежедневно начисляют сложные проценты, хотя вы можете узнать, что использует ваш конкретный эмитент, в информации о ценах вашей карты.
Найдите строку «Как мы рассчитаем ваш баланс». Если, например, эмитент использует метод, называемый «дневной баланс», это означает, что ваши проценты начисляются ежедневно.
Шаг 2. Разделите годовую процентную ставку (APR) вашей карты, чтобы получить периодическую ставку
Затем вам нужно найти периодическую ставку, которая поможет вам понять, сколько процентов вы платите по остатку за период.
Если ваш эмитент использует дневной баланс, вы разделите годовую процентную ставку на 365 дней. Если годовая процентная ставка начисляется ежемесячно, разделите ее на 12 месяцев. Например, годовая процентная ставка в размере 14,99% за день будет иметь периодическую ставку (14,99% / 365) = 0,00041 или 0.041% . Этот процент представляет собой вашу периодическую ставку, которая представляет собой годовую процентную ставку, деленную на количество периодов на вашем балансе.
Например, годовая процентная ставка в размере 14,99% за день будет иметь периодическую ставку (14,99% / 365) = 0,00041 или 0.041% . Этот процент представляет собой вашу периодическую ставку, которая представляет собой годовую процентную ставку, деленную на количество периодов на вашем балансе.
Периодическая скорость
Годовая / количество периодов
Шаг 3. Найдите свой средний дневной баланс
Чтобы узнать свой средний дневной остаток, вам необходимо точно знать, каким был ваш остаток на конец дня каждый день в рамках платежного цикла. Это может быть самой сложной частью расчета ваших процентов, поскольку ваш баланс может меняться изо дня в день и может стать особенно сложным, если вы часто пользуетесь своей картой.(Если вы будете вносить новые платежи на свою карту каждый день в месяц, состоящий из 31 дня, вам придется рассчитывать остаток на конец дня для 31 отдельного дня.)
Например, предположим, что на вашей карте было 300 долларов США в течение первых трех дней, 500 долларов США в течение следующих 15 дней и, наконец, до 1000 долларов США за последние семь дней. Ваш средний дневной баланс составит 616 долларов. Это число рассчитывается по следующей формуле:
Ваш средний дневной баланс составит 616 долларов. Это число рассчитывается по следующей формуле:
Среднедневной остаток
(остаток дня 1 + остаток дня 2 + остаток дня 3…) / общее количество дней в платежном цикле
Шаг 4. Соберите все вместе
Теперь вы готовы собрать все воедино.Вы умножите периодическую ставку из шага 2 на средний дневной баланс из шага 3 и количество дней в вашем платежном цикле. Результатом являются проценты, начисленные по кредитной карте за определенный период.
По большинству кредитных карт будет взиматься минимальная процентная плата. Сумма варьируется в зависимости от банка, но обычно составляет от 1 до 2 долларов. Таким образом, если вы следуете приведенным здесь расчетам и получаете процентную плату в размере 0,50 доллара США, вместо нее вы будете платить минимальную процентную плату.
Пример расчета
Чтобы помочь вам наглядно представить эту формулу, мы предоставили пример расчета для карты, по которой начисляются проценты по дневному остатку. Мы предполагаем, что эта карта имеет годовую ставку 14,99%. Вот активность карты за данный месяц:
Мы предполагаем, что эта карта имеет годовую ставку 14,99%. Вот активность карты за данный месяц:
| 1-4 | Нет | 0 долл. | |
| 5-10 | 200 долл. Покупка | 200 долл. 500 долларов при покупке | 750 долларов |
| 19 | 400 долларов при оплате | 350 долларов | |
| 20-25 | 200 долларов при покупке | 550 долларов |
{«alignsHorizontal»: [], «alignsVertical»: [], «columnWidths»: [], «data»: [[«День», «Активность», «Баланс»], [«1-4″, » Нет »,« 0 долларов »], [« 5–10 »,« покупка на 200 долларов »,« 200 долларов »], [« 11–13 »,« покупка на 50 долларов »,« 250 долларов »], [« 14–18 »,« Покупка на 500 долларов »,« 750 долларов »], [« 19 »,« Платеж на 400 долларов »,« 350 долларов США »], [« 20–25 долларов США »,« Покупка на 200 долларов США »,« 550 долларов США »]],« сноска »:« «,» hasMarginBottom «: true,» isExpandable «: true,» isSortable «: false,» maxWidth «:» 1215 «,» minWidth «:» 100% «,» showSearch «: false,» sortColumnIndex «: 0,» sortDirection «: «asc»}
Для вычисления среднего дневного баланса , мы умножаем количество дней на его остаток на конец дня.
((4 * 0 долларов) + (6 * 200 долларов) + (3 * 250 долларов) + (5 * 750 долларов) + (1 * 350 долларов) + (6 * 550 долларов)) / 25 дней = 374 долларов
Для расчета процентов за 25-дневный период мы умножаем средний дневной остаток на дневную периодическую ставку и количество дней в платежном цикле.
| Ежедневная периодическая ставка | 14,99% / 365 | 0,041% |
| Средний дневной остаток | ((5 * 0 долларов США) + (6 * 200 долларов США) + (3 * 250 долларов США) + (5 * 750 долларов США) + ( 1 * 350 долларов США) + (6 * 550 долларов США)) / 25 дней = 374 доллара США | 374 доллара США |
| Количество дней в платежном цикле | Дни 1-25 | 25 |
| Проценты рассчитано | 374 $ * 25 * 0. 041% 041% | 3,83 долл. США |
{«alignsHorizontal»: [], «alignsVertical»: [], «columnWidths»: [], «data»: [[«Фактор», «Расчет», «Результат»], [«Периодическая дневная скорость», » 14,99% \ / 365 «,» 0,041% «], [» Средний дневной баланс «,» ((5 * 0 долларов США) + (6 * 200 долларов США) + (3 * 250 долларов США) + (5 * 750 долларов США) + (\ u003Cem \ u003E1 \ u003C \ / em \ u003E * 350 $) + (6 * 550 $)) \ / 25 дней = \ u003Cstrong \ u003E $ 374 \ u003C \ / strong \ u003E «,» 374 $ «], [» Количество дней в платежном цикле «,» Дни 1-25 «,» 25 «], [» \ u003Cstrong \ u003EРассчитанный процент \ u003C \ / strong \ u003E «,» \ u003Cstrong \ u003E $ 374 * 25 * 0.041% \ u003C \ / strong \ u003E «,» \ u003Cstrong \ u003E $ 3.83 \ u003C \ / strong \ u003E «]],» footnote «:» «,» hasMarginBottom «: true,» isExpandable «: true,» isSortable » : false, «maxWidth»: «1215», «minWidth»: «100%», «showSearch»: false, «sortColumnIndex»: 0, «sortDirection»: «asc»}
Чтобы вычислить дневную периодическую ставку , мы разделим годовую процентную ставку на 365 дней (14,99% / 365 = 0,041%).
Поскольку в платежном цикле 25 дней, теперь мы можем сложить все эти числа вместе. Мы умножаем средний дневной баланс, дневную периодическую ставку и количество дней в платежном цикле, чтобы получить проценты в размере 3 долларов.83.
Что нужно знать о льготных периодах кредитной карты
Если вы хотите полностью избежать задолженности по кредитной карте, эмитенты обычно предлагают держателям карт определенный период времени для погашения их баланса. В течение этого льготного периода на любые новые покупки, добавленные на баланс, проценты не начисляются. Оплачивая счет по кредитной карте в течение этого льготного периода, с вас не будут взиматься никакие проценты.
В соответствии с Законом о картах от 2009 года у вас есть 21 день на выплату остатка до начала начисления процентов.Это время применяется с момента доставки вам счета по почте или в электронном виде. Если срок сдачи выпадает на выходные или государственный праздник, у вас будет время до 17:00 следующего рабочего дня. для отправки платежа.
для отправки платежа.
Инструменты, помогающие визуализировать проценты по кредитной карте
Теперь, когда вы понимаете, как работают проценты по кредитной карте, вы можете использовать автоматизированный инструмент, который упростит ваши расчеты. Наш калькулятор процентов по кредитной карте позволяет вам добавить столько остатков по кредитной карте, сколько вы хотите ниже, вместе с их процентными ставками и типом ежемесячных платежей, которые вы производите.Калькулятор покажет, какими будут ваши общие процентные платежи к тому моменту, когда вы полностью погасите свой долг.
Калькулятор процентов по кредитной карте
остаток
платеж
проценты (годовые)
время выплаты
Визуализация вашей долговой нагрузки
Чтобы помочь вам отслеживать, насколько быстро ваш баланс будет затронут в соответствии с вашим текущим планом платежей, мы построили графики ваш прогресс с течением времени ниже.
{«onCurrent»: «true»}
Приговор Пингвина
Распространенное заблуждение состоит в том, что годовая процентная ставка (APR) означает, что проценты по кредитной карте рассчитываются каждый год. Вместо этого большинство эмитентов ежедневно начисляют проценты. Следовательно, важно знать, сколько процентов вы будете получать, если каждый месяц будете иметь остаток на своей карте.
Вы также можете использовать любой из наших инструментов для расчета этих процентов, если вы предпочитаете не рассчитывать эти ставки вручную.Прежде всего, важно ежемесячно оплачивать остаток в полном объеме, чтобы полностью избежать процентных платежей.
Как преобразовать годовую процентную ставку в месячную | Малый бизнес
Автор: Эшли Адамс-Мотт Обновлено 22 октября 2018 г.
Знание того, как преобразовать годовую процентную ставку в ежемесячную, позволит вашему бизнесу рассчитать процентные расходы по ссуде, подлежащей ежемесячному начислению сложных процентов. С помощью этой метрики вы можете ежемесячно оценивать расходы по ссуде, а калькулятор эффективной процентной ставки позволяет просматривать стоимость на годовой основе.Когда вам нужно занять деньги для расширения своего малого бизнеса или инвестирования средств, эти расчеты помогут вам найти лучший вариант.
С помощью этой метрики вы можете ежемесячно оценивать расходы по ссуде, а калькулятор эффективной процентной ставки позволяет просматривать стоимость на годовой основе.Когда вам нужно занять деньги для расширения своего малого бизнеса или инвестирования средств, эти расчеты помогут вам найти лучший вариант.
Компоненты финансовых формул
Большинство финансовых расчетов и формул основываются на нескольких базовых данных, включая процентную ставку и количество периодов платежей. Формулы для расчета ежемесячной процентной ставки и эффективной годовой ставки основываются на заявленной процентной ставке, которая выражается переменной «i». Если вы не уверены в своей годовой процентной ставке, посмотрите свой последний отчет или исходную ссуду.Количество периодов оплаты выражается переменной «n». Для расчета ежемесячной процентной ставки «n» представляет количество месяцев в году, или 12.
В других формулах это может представлять количество периодов выплат в течение срока ссуды, например 120 платежей в 10 -годовая ссуда. Если вы рассчитываете свою ежемесячную ставку по годовой процентной ставке, всегда используйте 12 периодов — даже если ваш кредит рассчитан на меньший период времени, например шесть месяцев, или более длительный период, например три года.
Если вы рассчитываете свою ежемесячную ставку по годовой процентной ставке, всегда используйте 12 периодов — даже если ваш кредит рассчитан на меньший период времени, например шесть месяцев, или более длительный период, например три года.
Преобразование годовых в месячные
Чтобы преобразовать годовую процентную ставку в ежемесячную, используйте формулу «i», разделенную на «n», или процент, разделенный на периоды выплат.Например, чтобы определить ежемесячную ставку по ссуде в размере 1200 долларов США с выплатой в течение одного года и 10-процентной годовой ставкой, разделите ее на 12 или 10 ÷ 12, чтобы получить 0,0083 процента в качестве месячной ставки. При балансе в 1200 долларов процентная ставка за первый месяц будет определяться путем умножения месячной ставки на общую сумму, или 1200 долларов на 0,0083, чтобы получить 9,96 доллара.
Графики погашения и проценты
Этот простой расчет позволяет взглянуть на базовые расчеты процентов, но многие ссуды содержат более сложные графики погашения. С этими планами платежей ссуды имеют фиксированный ежемесячный платеж. В течение срока кредита большая часть ваших процентов выплачивается в начале периода кредита. По мере того, как срок ссуды истекает, соотношение меняется к более крупным выплатам основной суммы долга. Если ваша цель — ограничить выплату процентов по своим кредитам, по возможности делайте дополнительные платежи и попросите свой банк применить дополнительный платеж к основной сумме долга. Вам также необходимо будет обратиться к своему графику погашения, чтобы правильно отразить ежемесячные расходы в ваших финансовых отчетах.
С этими планами платежей ссуды имеют фиксированный ежемесячный платеж. В течение срока кредита большая часть ваших процентов выплачивается в начале периода кредита. По мере того, как срок ссуды истекает, соотношение меняется к более крупным выплатам основной суммы долга. Если ваша цель — ограничить выплату процентов по своим кредитам, по возможности делайте дополнительные платежи и попросите свой банк применить дополнительный платеж к основной сумме долга. Вам также необходимо будет обратиться к своему графику погашения, чтобы правильно отразить ежемесячные расходы в ваших финансовых отчетах.
Эффективные годовые ставки
Когда ваши проценты по ссуде рассчитываются ежемесячно, они складываются, и вы в конечном итоге платите проценты по ранее начисленным процентам. Из-за этого заявленная годовая процентная ставка, которую вы платите по ссуде, на самом деле меньше, чем общее влияние процентов на вашу прибыль. Если вы рассчитываете свою ежемесячную процентную ставку, пытаясь оценить варианты ссуды, важно также проанализировать эффективную ставку. n -1.12 = 1,1043
n -1.12 = 1,1043
Чтобы умножить элемент в степени другого числа, нужно умножить его на себя указанное количество раз. В этом примере 1,0083 умножается на само себя 12 раз, чтобы получить 1,1043. Если у вас есть доступ к научному калькулятору, вы можете использовать кнопку экспоненты, чтобы упростить этот расчет.
Как рассчитать годовую процентную ставку | Indeed.com
Заимствование средств у учреждения или кредитование связано с расходами.Банки и финансовые учреждения зарабатывают деньги на депозитах, которые люди оставляют на их попечении. Они получают прибыль, взимая с людей, которые занимают у них, определенный процент от заемных денег. В этой статье мы объясним, что такое APR, типы APR и как его рассчитать.
Связано: Значение увеличения вашего бизнес-словаря
Что такое годовая процентная ставка?
Годовая процентная ставка или годовая процентная ставка — это общая стоимость заимствования у финансового учреждения в течение одного года. Годовая процентная ставка — хороший способ рассчитать стоимость заимствования, поскольку она учитывает все связанные с заимствованием затраты, включая дополнительные расходы, такие как штрафы за просрочку платежа, сборы за закрытие сделки и административные сборы.
Годовая процентная ставка — хороший способ рассчитать стоимость заимствования, поскольку она учитывает все связанные с заимствованием затраты, включая дополнительные расходы, такие как штрафы за просрочку платежа, сборы за закрытие сделки и административные сборы.
APR не учитывает сложный эффект процентов, если он применяется. Годовая процентная ставка используется для сравнения затрат разных кредиторов.
Связано: Ваш путеводитель по карьере в области финансов
Типы годовых
Существует два типа годовых:
- Фиксированная годовая процентная ставка: В фиксированной годовой процентной ставке применяется процентная ставка к основной сумме займа не меняется.Годовая процентная ставка, рассчитанная на основе процентной ставки, также будет фиксированной. Ставка не меняется, поэтому сумма, выплачиваемая в год за заимствование этих денег, остается неизменной.
- Переменная годовая процентная ставка: Переменная годовая процентная ставка может изменяться, поскольку процентная ставка, применяемая к основной сумме долга, время от времени меняется.
 Это зависит от движения основной кредитной ставки в США. Переменный характер означает, что при резком повышении процентной ставки заемщик платит больше.
Это зависит от движения основной кредитной ставки в США. Переменный характер означает, что при резком повышении процентной ставки заемщик платит больше.
Чем выше годовая процентная ставка, тем больше процентов выплачивает заемщик.Держатели кредитных карт, которые оплачивают свои счета полностью и вовремя, как правило, не подвержены влиянию годовой процентной ставки. Это потому, что годовая процентная ставка рассчитывается на основе остатка. Если остаток выплачен полностью и вовремя, годовая процентная ставка не применяется.
Как рассчитать APR
Чтобы рассчитать APR по ссуде, вам необходимо принять во внимание основную сумму, количество лет, в течение которых ссуда будет длиться, и дополнительные расходы, которые несет ссуда в дополнение к процентам.
Для расчета годовой процентной ставки выполните следующие действия:
- Рассчитайте процентную ставку
- Добавьте административные сборы к сумме процентов
- Разделите на сумму ссуды (основную сумму)
- Разделите на общее количество дней в сроке ссуды
- Умножьте все на 365 (один год)
- Умножьте на 100, чтобы преобразовать в процент
Вот формула годовой процентной ставки:
Годовая процентная ставка = ((Проценты + Комиссия / сумма займа) / Количество дней в ссуде срок)) x 365 x 100
Например, Фрэнсис занимает 2000 долларов под 5% годовых сроком на два года. Заключительные административные расходы по ссуде составляют 200 долларов США. Чтобы определить годовую процентную ставку, сначала рассчитайте процент по этой ссуде, используя простую формулу процентов: A = (P (1 + RT), где A = общая начисленная сумма, P = основная сумма, R = процентная ставка и T = период времени.
Заключительные административные расходы по ссуде составляют 200 долларов США. Чтобы определить годовую процентную ставку, сначала рассчитайте процент по этой ссуде, используя простую формулу процентов: A = (P (1 + RT), где A = общая начисленная сумма, P = основная сумма, R = процентная ставка и T = период времени.
В данном случае P = 2000 долларов США, R = 5% и T = 2 года. Следовательно, A = (2000 (1 + 0,05×2)) или A = 2200 долларов США.
Начисленные проценты = A — P = 2200 долларов США — 2000 долларов США. и проценты = 200 долл.
Затем добавьте проценты к затратам на закрытие. Используя формулу годовой процентной ставки, сборы + проценты = 200 долл. США + 200 долл. США = 400 долл. США.
Наконец, разделите сумму ссуды и количество периодов, затем умножьте на 100, чтобы получить процент.
Годовая процентная ставка = (400/2000) / 2 x 1 x 100 = 10%
Годовая процентная ставка по данному кредиту составляет 10%.
Из расчетов годовой процентной ставки вы можете обнаружить, что даже если кажется, что процентная ставка по этой ссуде составляет 5%, реальная годовая стоимость этой ссуды составляет 10% с учетом всех сборов.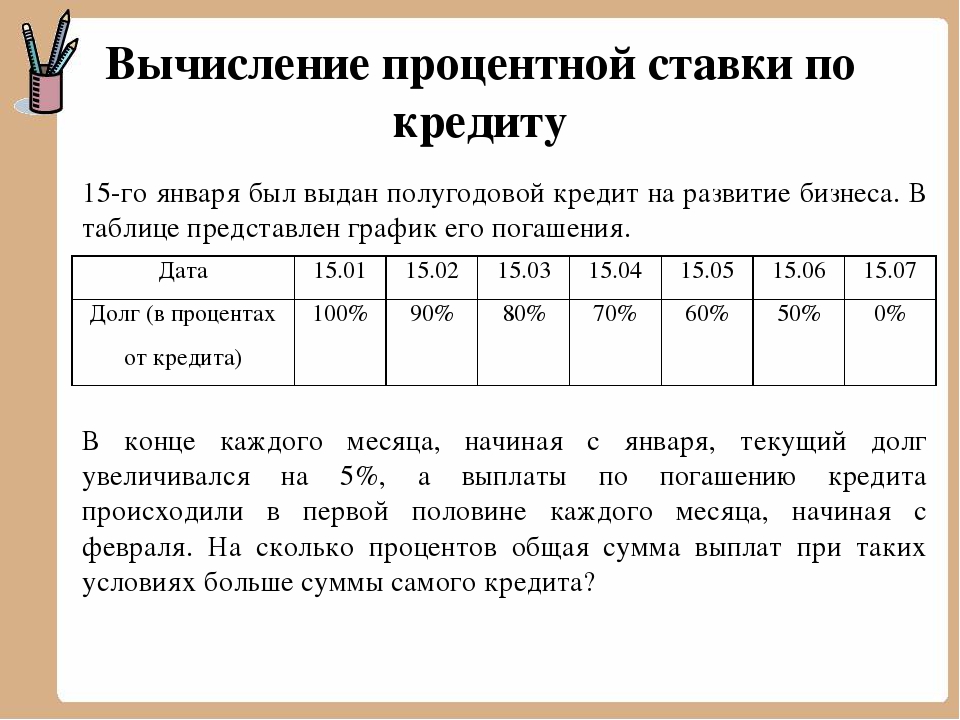
Связанные: 6 основных навыков бухгалтерского учета
Годовая процентная ставка vs.APY
Хотя годовая процентная ставка дает вам реальную стоимость ссуды ежегодно, она не учитывает сложный эффект ссуды, когда ссуда не рассчитывается на основе простых процентов, как показано выше.
Вышеприведенный расчет процентных выплат основан на простой процентной модели, которая не широко используется для долгосрочных кредитов, таких как студенческие или ипотечные кредиты.
Чтобы учесть эффект сложного процента от ссуды, вы можете использовать годовой процентный доход (APY) вместо APR.
Годовая процентная доходность — это сумма, которая зарабатывается на сберегательном вкладе с учетом сложного характера сложных процентов. Годовая процентная доходность дает общую сумму, которую сбережения или инвестиции принесут за период.
По сравнению с годовой процентной ставкой годовая доходность измеряет, что кредитор получит, вложив свои деньги, с учетом того, сколько раз инвестиции были усугублены. (365 / дней в срок ссуды) -1]
(365 / дней в срок ссуды) -1]
Например, Фрэнсис получила проценты в размере 40 долларов за внесение 2000 долларов в банк.(365/365) -1]
Годовая процентная доходность составляет 2%.
Годовая процентная ставка к номинальной процентной ставке
Номинальная процентная ставка — это процентная ставка без учета инфляции. Это не реальная процентная ставка, используемая банковскими учреждениями. Номинальная процентная ставка с поправкой на инфляцию становится реальной процентной ставкой, которая обычно отличается от номинальной процентной ставки.
Когда банки рекламируют свои процентные ставки, обычно рекламируются номинальные ставки.Номинальные ставки — это базовые ставки, которые банки используют для кредитования.
Когда вкладчики делают депозит или инвестируют в банк, они рассчитывают заработать на своих вложениях. Заработанная сумма определяется реальной процентной ставкой, а не номинальной процентной ставкой.
Реальная процентная ставка может увеличиваться или уменьшаться. Когда происходит рост, вкладчик зарабатывает больше денег, а если реальные ставки падают, они делают меньше.
Когда происходит рост, вкладчик зарабатывает больше денег, а если реальные ставки падают, они делают меньше.
Ключевые различия между годовой процентной ставкой и номинальной процентной ставкой
Есть несколько ключевых различий между годовой процентной ставкой и номинальной процентной ставкой, в том числе следующее:
- Годовая процентная ставка рассчитывает общую стоимость заимствования в год, в то время как номинальная процентная ставка это процентная ставка, которую привлекает заемная сумма.
- Годовая процентная ставка использует реальную процентную ставку, скорректированную с учетом инфляции, а также включает другие вспомогательные административные расходы по займам в год. Номинальная процентная ставка не учитывает инфляцию.
- Годовая процентная ставка используется для реалистичного сравнения ссуд для заемщика, в то время как номинальная процентная ставка, используемая для сравнения ссуд, может быть неточной.
Недостатки
годовых, будучи хорошим показателем для расчета общей стоимости заимствования, также имеет недостатки, которые делают его несовершенным для сравнения ссуд. Ниже приведены основные недостатки использования одной только годовой процентной ставки в качестве сравнительного показателя при выборе пакета ссуды:
Ниже приведены основные недостатки использования одной только годовой процентной ставки в качестве сравнительного показателя при выборе пакета ссуды:
- годовая процентная ставка работает только тогда, когда вы знаете, что выплатите ссуду в полном объеме. Если вы планируете рефинансировать ссуду на полпути, условия получения новой годовой процентной ставки от другого кредитора могут измениться, что сделает ваши первоначальные расчеты годовой процентной ставки бесполезными.
- Годовая процентная ставка отличается от кредитора к кредитору. При покупке кредита важно проверить все предлагаемые ставки, особенно с учетом дополнительных расходов и переменных процентных ставок.Если процентная ставка переменная, годовая процентная ставка может быть неточной, поскольку любое изменение процентной ставки повлияет на общую стоимость ссуды.
- Годовая процентная ставка не учитывает сложный эффект процентных ставок. Если при выборе ссуды возникает сложный эффект процентной ставки, годовая процентная ставка не будет хорошим индикатором стоимости.

Как рассчитать эффективную годовую процентную ставку
Интересующие вопросы могут не интересовать многих. Многие люди паникуют, когда дело доходит до сложного финансового жаргона и сокращений.Тем не менее, если вы занимаетесь предоставлением кредитов, важно понимать, как рассчитываются процентные ставки. В самом деле, если вы ведете бизнес, в котором используются кредиты (что вы почти наверняка делаете), это также важно понимать. Здесь мы рассмотрим, как рассчитать эффективную годовую процентную ставку (EAR), чтобы вы могли лучше понять проценты, подлежащие выплате (или полученные) по кредиту, который вы предлагаете и используете.
Что такое эффективная годовая процентная ставка?
Чтобы лучше понять реальное влияние процентов на наш бизнес, нам необходимо принимать во внимание комплексные проценты.Всякий раз, когда рекламируются процентные ставки (номинальные ставки), начисление сложных процентов не учитывается. Но если мы не сделаем это сами, у нас могут остаться неточные прогнозы денежных потоков и вероятность пропущенных или просроченных платежей, которые могут повлечь за собой дополнительные расходы и еще больше поставить под угрозу нашу ликвидность.
Проще говоря, EAR — это проценты, которые выплачиваются в реальном выражении по любой ссуде, кредитной карте или другому долгу, который вы предоставляете или используете. Это то, что вы используете для расчета своих доходов по кредиту, который вы предоставляете своим клиентам, или ваших реальных обязательств перед кредиторами.
Понимание формулы EAR
Несмотря на то, что существует полезный калькулятор эффективной годовой процентной ставки, который может автоматизировать этот процесс, важно знать формулу самостоятельно. Это требует от вас понимания двух переменных. Объявленная номинальная годовая процентная ставка (которую мы будем называть r) и количество периодов, в течение которых начисляются проценты (i). Поскольку обычно это месяцы, мы будем обозначать это как m.
Таким образом, формула для расчета EAR (которую мы будем называть i) выглядит так:
i = (1 + r / m) xm −1
Чем больше у вас периодов начисления сложных процентов, тем больше вы можете ожидать, что ваш EAR увеличится.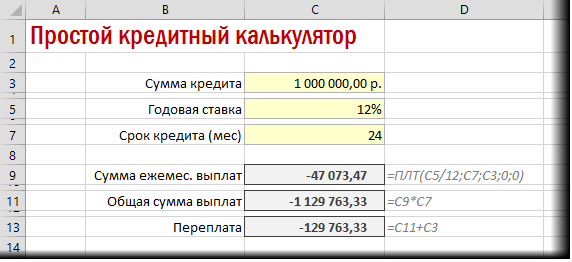 Таким образом, ежеквартальное начисление сложных процентов дает более высокую прибыль, чем начисление сложных процентов каждые шесть месяцев, в то время как ежемесячное начисление сложных процентов дает больше, чем ежеквартально. Некоторые кредиторы даже ежедневно прибавляют.
Таким образом, ежеквартальное начисление сложных процентов дает более высокую прибыль, чем начисление сложных процентов каждые шесть месяцев, в то время как ежемесячное начисление сложных процентов дает больше, чем ежеквартально. Некоторые кредиторы даже ежедневно прибавляют.
Конечно, если вы не слишком разбираетесь в математике, эту формулу может быть сложно контекстуализировать. Итак, давайте рассмотрим наглядный пример.
Пример эффективной годовой процентной ставки
Допустим, вам необходимо новое оборудование для вашей компании. Вы знаете, что это оборудование будет стоить вам 5000 долларов, но у вас недостаточно ликвидности, чтобы покрыть эту стоимость, не нарушив ваш денежный поток.(количество периодов начисления сложных процентов) — 1
Для банка A это будет: 10,47% = (1 + (10% / 12)) x 12 — 1
Для банка B это будет: 10,36 % = (1 + (10,1% / 2)) x 2 — 1
Итак, хотя у банка B может быть немного более высокая номинальная процентная ставка, у него более низкий EAR, чем у банка A, потому что он составляет меньше раз в течение курса года. Хотя эта разница может привести только к экономии 5,80 долларов в год по ссуде на 5000 долларов, если вам нужно было занять значительно больше, разница может действительно возрасти!
Хотя эта разница может привести только к экономии 5,80 долларов в год по ссуде на 5000 долларов, если вам нужно было занять значительно больше, разница может действительно возрасти!
Мы можем помочь
Если вы хотите узнать больше о расчете эффективной годовой процентной ставки, свяжитесь с финансовыми экспертами GoCardless.Узнайте, как GoCardless может помочь вам со специальными или регулярными платежами.
GoCardless используется более чем 55 000 компаний по всему миру. Узнайте больше о том, как вы можете улучшить обработку платежей в своем бизнесе уже сегодня.
Узнать больше Зарегистрироваться
Калькулятор годовых
При подаче заявки на ссуду, помимо процентов, кредиторы нередко взимают дополнительные комиссии или баллы. Реальная годовая процентная ставка учитывает эти расходы, а также процентную ставку по ссуде.Следующие два калькулятора помогают определить истинную стоимость ссуд через реальную годовую процентную ставку.
Калькулятор общей годовой процентной ставки
Реальная годовая процентная ставка: 6,335%
| Финансируемая сумма | 100 000,00 долларов США |
| Плата за предоплату | 1500,00 долларов США |
| из 120 платежей | 133 224,60 долл. США США |
| Итого проценты | 33 224 долл. США.60 |
| Все платежи и сборы | 134 724,60 долл. США |
Калькулятор годовых по ипотеке
Воспользуйтесь калькулятором ниже для ипотечного кредита в США.
Реальная годовая процентная ставка: 4,608%
| Сумма займа | 200 000,00 долларов США | ||||||
| Первоначальный взнос | 50 000,00 долларов США | ||||||
| 1,0 Ежемесячная плата | 32337|||||||
| Всего 360 платежей | 364 813,42 долл. США | ||||||
| Итого проценты | 164 813,42 долл. США | ||||||
| Все платежи и сборы ,4 | |||||||
|
|
Сборы, обычно не облагаемые годовой процентной ставкой, составляют:
- Стоимость экспертизы
- Гарантия строителя
- Предоплаченные позиции на счетах условного депонирования, такие как налоги или страхование
- Нематериальный налог
- Титульный осмотр
Годовая процентная ставка может быть фиксированной или переменной, и у каждого есть свои плюсы и минусы.
Фиксированная ставка
Ссуды с фиксированной годовой процентной ставкой содержат ставки, которые гарантированно не изменятся в течение срока ссуды. Для заемщика, получившего чрезвычайно заманчивую фиксированную процентную ставку, было бы разумно зафиксировать ее в период относительно низких рыночных процентных ставок, которые, как ожидается, будут повышаться позже. Фиксированные ставки обычно выше переменных ставок на момент предоставления кредита.
Переменная ставка
Ссуды с переменной годовой процентной ставкой имеют ставки, которые могут измениться в любое время, обычно из-за их корреляции с индексом.Например, если рыночные процентные ставки повышаются, большую часть времени переменные годовые процентные ставки, привязанные к кредитам, будут расти. Существует еще один компонент переменной годовой процентной ставки, называемый кредитной маржей, созданный кредитором. Это всего лишь модное слово для обозначения части предложения с расширенной переменной годовой процентной ставкой потенциальному заемщику, определяемой не рыночным индексом, а кредитоспособностью заемщика. Включение кредитной маржи для оценки переменных ставок для каждого отдельного лица не позволяет заемщикам с плохой кредитоспособностью пользоваться преимуществами системы, любезно предлагающей гибкость.Например, переменные ставки, вероятно, лучше подходят для тех, кто взял ссуду при относительно высоких рыночных ставках, которые, по прогнозам, будут снижаться. Исторические данные показали, что заемщики, как правило, платили меньше процентов, используя переменную ставку, а не фиксированную.
Включение кредитной маржи для оценки переменных ставок для каждого отдельного лица не позволяет заемщикам с плохой кредитоспособностью пользоваться преимуществами системы, любезно предлагающей гибкость.Например, переменные ставки, вероятно, лучше подходят для тех, кто взял ссуду при относительно высоких рыночных ставках, которые, по прогнозам, будут снижаться. Исторические данные показали, что заемщики, как правило, платили меньше процентов, используя переменную ставку, а не фиксированную.
В любом случае важно учитывать срок кредита. Как правило, чем дольше срок ссуды, например, ипотеки на тридцать лет, тем сильнее влияние колебаний ставки.
APR по сравнению с APY
Потенциальным заемщикам может быть полезно различать APR и APY, которые представляют собой годовую процентную доходность, термин, который в основном ассоциируется с депозитными счетами.APY — это ставка, которая отражает общую сумму процентов, выплачиваемых по счету, на основе заданной процентной ставки и частоты начисления сложных процентов в течение 365-дневного периода. APY иногда называют EAPR, эффективной годовой процентной ставкой, или EAR, эффективной годовой ставкой. Основное различие между ними и годовой процентной ставкой состоит в том, что в первом случае учитываются сложные проценты, а в годовом — нет. Поскольку финансовые учреждения хотят рекламировать наиболее привлекательные ставки для своей клиентуры, заемщикам предоставляются ставки годовых вместо годовых, потому что ставки ниже, тогда как владельцам сберегательных счетов будут рекламироваться ставки годовых, поскольку они выше из-за начисляемых процентов.Например, если для компакт-диска за 100 долларов процентная ставка составляет 10%, процент, полученный в конце года, составит:
APY иногда называют EAPR, эффективной годовой процентной ставкой, или EAR, эффективной годовой ставкой. Основное различие между ними и годовой процентной ставкой состоит в том, что в первом случае учитываются сложные проценты, а в годовом — нет. Поскольку финансовые учреждения хотят рекламировать наиболее привлекательные ставки для своей клиентуры, заемщикам предоставляются ставки годовых вместо годовых, потому что ставки ниже, тогда как владельцам сберегательных счетов будут рекламироваться ставки годовых, поскольку они выше из-за начисляемых процентов.Например, если для компакт-диска за 100 долларов процентная ставка составляет 10%, процент, полученный в конце года, составит:
$ 100 × 10% = 10
$Получено 10 процентов в виде процентов. Для сравнения, если заем в 100 долларов взят под 10% годовых, можно рассчитать эквивалентные проценты, выплачиваемые в конце года. Если вы ищете только эффективную годовую процентную ставку, используйте следующую формулу:
Чтобы найти фактическую сумму выплаченных процентов, используйте вместо этого следующую формулу:
| Главный × ((1 + | ) n -1) |
| $ 100 × ((1 + | ) 12 — 1) = 10 долларов США.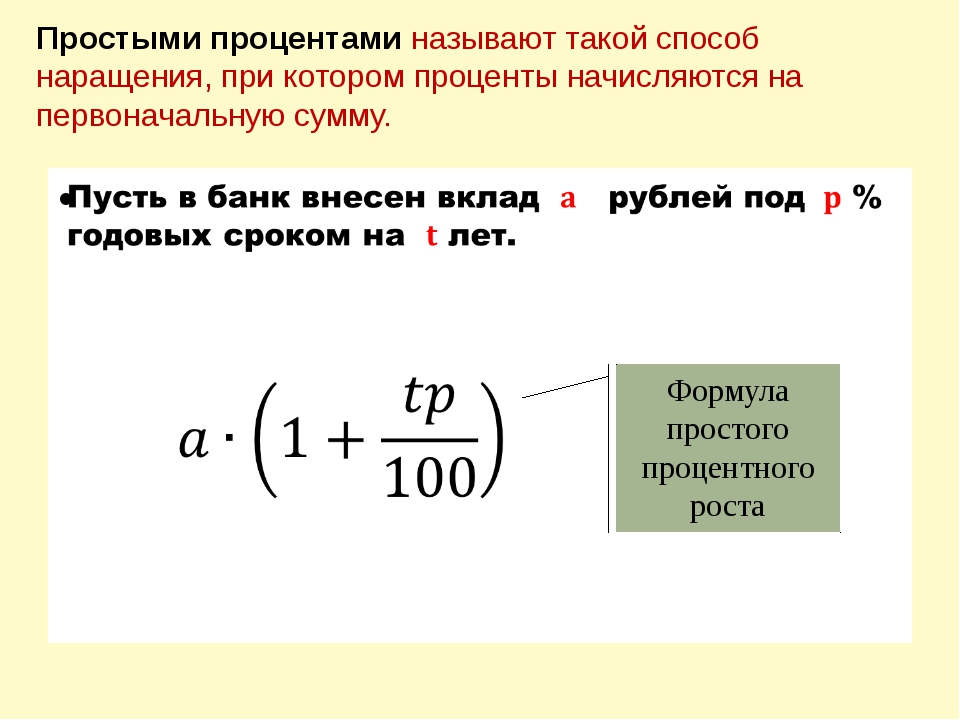 47 47 |
Будет выплачено 10,47 долларов США в виде процентов.
Калькулятор процентной ставки для сбережений или ссуд
Рассчитайте процентную ставку по ссуде или сбережениям, используя эти три калькулятора процентных ставок.
Какая у меня процентная ставка?
Воспользуйтесь нашим калькулятором процентных ставок, чтобы рассчитать процентную ставку, которую вы получаете по кредитным картам, займам, ипотеке или сбережениям. Процентная ставка — это процент, который кредитор взимает с заемщика за определенную сумму денег.Этот переводится как стоимость заимствования. Вы можете одалживать деньги у кого-то (заем) или давать им взаймы (сбережения или инвестиции).
Для общих типов сберегательных счетов и инвестиций вы будете получать сложные проценты на свой баланс. Это означает, что проценты начисляются сверх уже заработанных процентов, так как
а также первоначальный принципал. Поэтому при расчете получаемой процентной ставки вам необходимо сложить начальную номинальную процентную ставку, чтобы найти эффективную ставку, которая учитывает начисление сложных процентов.Конечно,
в некоторых случаях вы можете давать ссуду или получать деньги на основе простого расчета процентов без начисления сложных процентов. Это означает, что интерес только
рассчитывается на остаток, а не на ранее начисленные проценты.
Поэтому при расчете получаемой процентной ставки вам необходимо сложить начальную номинальную процентную ставку, чтобы найти эффективную ставку, которая учитывает начисление сложных процентов.Конечно,
в некоторых случаях вы можете давать ссуду или получать деньги на основе простого расчета процентов без начисления сложных процентов. Это означает, что интерес только
рассчитывается на остаток, а не на ранее начисленные проценты.
Какую процентную ставку я получаю по ссуде?
Для расчета процентной ставки, которую вы получаете по кредитной карте или ссуде, требуется серия вычислений, включающая сумму ссуды, количество произведенных платежей и либо ежемесячный платеж, либо уплаченные проценты.Наш калькулятор
использует метод Ньютона-Рафсона для расчета
процентные ставки по кредитам. Это сложный процесс, позволяющий получить более точную цифру процентной ставки. Метод Ньютона-Рафсона выбирает
ряд значений, которые нужно попробовать, а затем сходится к ответу, когда уравнение уравновешивается.
Независимо от того, взяли ли вы ипотеку или ссуду, бывает сложно определить процентную ставку, которую вы платите по ней. Здесь на помощь приходит наш калькулятор, который дает вам четкое представление о том, сколько вы, возможно, платите. Обратите внимание, что в нашем калькуляторе процентных ставок используется ежемесячное сложение .
Если вы хотите использовать электронную таблицу для расчета процентов, попробуйте эту простую электронную таблицу калькулятора ссуд от Vertex42.
Какую процентную ставку я получаю по своим инвестициям / сбережениям?
Для расчета нормы прибыли на инвестиционный или сберегательный баланс мы используем адаптированную версию
формула сложных процентов, используемая в наших калькуляторах.Мы вводим в формулу ваш текущий баланс, исходную основную сумму, количество соединений в год и период времени, и формула дает нам итоговую величину баланса.
У нас также есть другие варианты инвестиций, включающие расчет будущей стоимости и прибыли. Если вы хотите рассчитать процентную ставку, которую вы можете получить на инвестиции, на основе текущей стоимости и будущее значение, попробуйте калькулятор CAGR. Чтобы получить помощь в расчете окупаемости инвестиций, попробуйте калькулятор IRR
Какая номинальная процентная ставка?
Номинальная процентная ставка — это величина процентной ставки до учета поправки на инфляцию.Формула номинальной процентной ставки:
Номинальная процентная ставка = n × ((1 + r) 1 / n — 1) r = эффективная процентная ставка
n = количество периодов начисления сложных процентов
Какая эффективная процентная ставка?
Эффективная годовая ставка — это процентная ставка, полученная по ссуде или инвестициям за период времени, с учетом сложных процентов и . Его также можно назвать годовой эквивалентной ставкой (AER). Чтобы привести пример,
годовая процентная ставка 5% с ежемесячным начислением сложных процентов приведет к эффективной годовой ставке 5,12%. Это связано с тем, что ежемесячные проценты фактически начисляются поверх предыдущих ежемесячных процентов. Чем чаще проценты складываются в
период времени, тем выше будет эффективная годовая ставка.
Его также можно назвать годовой эквивалентной ставкой (AER). Чтобы привести пример,
годовая процентная ставка 5% с ежемесячным начислением сложных процентов приведет к эффективной годовой ставке 5,12%. Это связано с тем, что ежемесячные проценты фактически начисляются поверх предыдущих ежемесячных процентов. Чем чаще проценты складываются в
период времени, тем выше будет эффективная годовая ставка.
i = номинальная процентная ставка
n = количество периодов
Какая годовая процентная ставка по моей ссуде?
Годовая процентная ставка (APR) включает плату за установку, взимаемую вашим кредитором как часть вашего общего расчета процентов, в среднем за 12 месяцев.Это может дать представление о том, сколько именно ваша ипотека,
вам обходятся автокредиты или ссуды с фиксированной процентной ставкой.


 Поскольку расчет доходности прироста капитала включает рыночную цену ценной бумаги с течением времени, его можно использовать для анализа колебаний рыночной цены ценной бумаги. См. Расчет и пример
Поскольку расчет доходности прироста капитала включает рыночную цену ценной бумаги с течением времени, его можно использовать для анализа колебаний рыночной цены ценной бумаги. См. Расчет и пример Это зависит от движения основной кредитной ставки в США. Переменный характер означает, что при резком повышении процентной ставки заемщик платит больше.
Это зависит от движения основной кредитной ставки в США. Переменный характер означает, что при резком повышении процентной ставки заемщик платит больше.
 Хотя процентные ставки полезны, они не обеспечивают той точности, которую заемщик действительно хочет знать при определении, какая ставка для какого кредитора является наилучшей сделкой. Real APR делает это путем включения в процентную ставку любых других дополнительных расходов, связанных с ссудой. По большинству кредитов у кредиторов есть простор для маневра в отношении того, что они решили включить в годовую процентную ставку.
Хотя процентные ставки полезны, они не обеспечивают той точности, которую заемщик действительно хочет знать при определении, какая ставка для какого кредитора является наилучшей сделкой. Real APR делает это путем включения в процентную ставку любых других дополнительных расходов, связанных с ссудой. По большинству кредитов у кредиторов есть простор для маневра в отношении того, что они решили включить в годовую процентную ставку. Все эти затраты выглядят намного дешевле, если распределить по ипотеке на 30 лет, а не на быстрое ускоренное погашение через 10 лет.
Все эти затраты выглядят намного дешевле, если распределить по ипотеке на 30 лет, а не на быстрое ускоренное погашение через 10 лет.