Что такое сложные проценты? | Общество (июнь 2022)

• 17.06.2022

Рассматривая вопрос о том, куда вложить свои деньги, люди обычно ориентируются исключительно на процентную ставку. Это логично, так как чем выше процентная ставка, тем выше доходность инвестиций. Однако есть еще один фактор, который влияет на конечный результат, — это вид начисляемых процентов. На практике чаще всего используются простые проценты. Сложные проценты встречаются реже, но они позволяют получить больше прибыли за то же время.

Рассмотрим следующие вопросы:

• то такое сложные проценты?
• Как пользоваться калькулятором сложных процентов
• Как работает сложный процент?
• Часто задаваемые вопросы
• Что такое сложные проценты?

Сложные проценты — это проценты, которые начисляются как на первоначальную сумму, так и на проценты за предыдущий период, или проценты на проценты.

Например, если вы открываете вклад, то в первый год проценты будут начисляться на основную сумму вклада, во второй год — на сумму вклада и проценты, полученные в первый год, а в третий год — на все, что было заработано ранее.

Таким образом, получается, что каждый год депозит растет больше, чем в предыдущие годы. Например, если в предыдущем году он вырос на $100, то в этом году он может вырасти на $110, а в следующем — на $150. При сложной процентной ставке не бывает такого, чтобы каждый год был одинаковым.
Как пользоваться калькулятором сложных процентов

Введите начальную сумму

Это сумма, которую вы хотите использовать при создании депозита или при начале инвестирования. Обычно говорят, что это самый важный параметр, но на самом деле это не всегда так, иногда он является второстепенным фактором, например, когда темп высокий или периодичность темпа увеличивается.

Укажите дополненияЗдесь нужно указать сумму, которая будет периодически добавляться к начальной сумме. Например, после создания депозита некоторые банки позволяют пополнять счет через разные промежутки времени. Вот для чего нужно это поле. Если вы решили, что не хотите пополнять счет, введите 0.
Введите процент и период расчета

Один из самых важных параметров. Укажите процент, который будет взиматься за каждый выбранный период. Он определяет, сколько вы можете заработать за длительный период времени.

Укажите количество лет

Это количество лет, в течение которых вклад будет открыт. Это самое важное число при расчете сложных процентов. Чем дольше открыт вклад, тем больше вы сможете заработать, так как проценты начисляются ежегодно.

Нажмите кнопку «Рассчитать».Все, теперь при нажатии кнопки «Рассчитать» вы получите подробный график, формулу, объясняющую, как именно был произведен расчет (только на нашем сайте), и таблицу с результатами по каждому году.

Как работает сложный процент?

Сложные проценты предполагают использование первоначальной суммы и дохода, полученного в предыдущие периоды. Примером может служить депозит в банке, условия которого предусматривают капитализацию полученного дохода. Начисленная в первый месяц сумма процентов по вкладу зачисляется на основной счет, а во второй год проценты начисляются на увеличенную сумму, обеспечивая рост конечной доходности.

404 Cтраница не найдена

Версия для слабовидящих  Вход на сайт Версия для слабовидящих  Вход на сайт




Чукотский северо-восточный
техникум посёлка Провидения


• О техникуме
  • Сведения об образовательной организации
  • Образовательная организация
  • Аккредитация
  • Руководство
  • Преподаватели
  • Сотрудники
  • История
  • Документы
  • Устав
  • Библиотека и Библиотечно-информационная система
  • Контакты
  • Новости
  • Лицензии
  • Фотогалерея
  • Объявления
  • Газета «Роза Ветров»
  • Дорожная безопасность
  • Антикоррупционное просвещение
  • Центр коллективного доступа
  • Финансовая грамотность
  • Наставничество
  • Общественное питание
  • Воспитательная работа
• Абитуриентам
  • Приемная комиссия
  • Документы и справки
  • Правила и условия приема
  • Питание
  • Общежития
  • Студенческая жизнь
• Студентам
  • Учебные материалы
  • Оплата обучения
  • Документы и справки
  • Студенческая жизнь
  • Спортивная жизнь
  • Расписание занятий
  • Выпускникам
  • Справочные системы
• МЦПК
• Контакты
• Обращения граждан
  • Обращения граждан
  • Личный прием граждан
  • Письменное обращение
  • Электронная приемная
  • Проверить статус обращения
  • Порядок рассмотрения обращений
  • Порядок обжалования
  • Обзор обращений граждан
  • Ответы на обращения, затрагивающие интересы неопределенного круга лиц
  • Правовое регулирование
• Онлайн запись
• ССТВ
• Главная
• ›
• О техникуме
• ›
• Финансовая грамотность

Калькулятор сложных процентов: Депозитные сертификаты

Результаты обучения

• Расчет сложных процентов по времени
• Анализ и сравнение интереса к реальным приложениям

Депозитные сертификаты (CD) представляют собой долгосрочные сберегательные инструменты, предлагаемые банками. Они приходят с шагом, таким как один, три, пять или 10 лет. Идея состоит в том, что как только вы внесете свои деньги, вы оставите их нетронутыми в течение срока действия компакт-диска. Банки обычно готовы платить более высокие проценты в обмен на гарантию того, что ваши деньги будут использоваться дольше. Но компакт-диски имеют огромный штраф за досрочное снятие средств, поэтому вам нужно быть уверенным, что у вас есть деньги, чтобы выделить этот тип сбережений.

Вы можете легко найти годовую процентную доходность для компакт-дисков, рекламируемых на банковских веб-сайтах. См. образец ниже.

Обратите внимание, что рекламируется годовой доход в процентах, а не ставка. APY всегда будет немного больше, чем ставка из-за начисления сложных процентов. То есть проценты по вашему депозиту будут начисляться в фиксированные периоды в течение года и реинвестироваться. Вспомните формулу, приведенную ранее в тексте.

Сложные проценты

[латекс]P_{N}=P_{0}\left(1+\frac{r}{k}\right)^{Nk}[/latex]

• P _N остаток на счете после N лет.
• P ₀ — начальный баланс счета (также называемый начальным депозитом или основной суммой)
• r — годовая процентная ставка в десятичной форме
• k количество периодов начисления процентов в одном году

пример

Используйте формулу сложных процентов, чтобы найти APY для 5-летнего сертификата на сумму 1000 долларов со ставкой сложных процентов 1,44% в день. 9{k}-1[/latex]

Банки обычно рекламируют только APY, так как это более привлекательное число. Вы можете найти скорость, изучив детали компакт-диска.

Поскольку компакт-диски предназначены для того, чтобы вы могли оставить свои сбережения на весь срок, они представляют собой отличные примеры для изучения сложных процентов.

Электронная таблица Практическое занятие: создание калькулятора сложных процентов

Шаг 1. Создание калькулятора

Хорошей новостью является то, что мы уже проделали большую часть работы по созданию наших калькуляторов. (B5*B6). Обратите внимание, что Формула шаблона справа от этой ячейки также была изменена на сложные проценты.

• Нам также нужно изменить формулу в разделе «Проценты» с простых процентов на сложные проценты. Поскольку сложные проценты реинвестируются в течение срока действия компакт-диска, накопленные проценты не являются постоянными из года в год. Нам понадобится только одна процентная линия. Удалите строки 11 и 12, выбрав их, щелкнув правой кнопкой мыши и выбрав «Удалить». Измените описание процентов в C10 на «общие полученные проценты»
.
• Ответом в ячейке B10 будет разница между балансом и основной суммой: =B8-B3. Когда вы закончите, это должно выглядеть как на картинке ниже.

пример

Часто есть несколько хороших способов представления общей формулы. Например, разница между балансом CD в конце срока и первоначальным депозитом указана выше просто как разница между ячейками B8 и B3. И формула справа от ячейки B12 для общей суммы заработанных процентов также представляет собой простую разницу. Используйте алгебру, чтобы упростить эту формулу до общей формулы для общего заработанного процента.

Решение

Мы также можем включать ячейки, чтобы делать предположения о ситуациях со сложными процентами. Если мы хотим задать вопросы о скорости или времени с учетом других переменных, нам нужно изменить формулу. См. Примеры ниже для получения результатов и пошаговых решений. 9{\left(\frac{1}{Nk}\right)}-1\right][/latex]

Решение

Теперь у нас есть формулы для ввода второй части калькулятора.

1. Во-первых, нам нужно освободить место для включения периодов, поскольку наши формулы зависят от количества периодов начисления сложных процентов. Чтобы добавить строку, щелкните правой кнопкой мыши заштрихованную цифру «16» в строке 16 листа. Должно появиться меню, в котором вы можете нажать «вставить», чтобы вставить новую строку ниже строки 15. Назовите эту строку периодами.
2. Нам нужно заполнить эти ячейки значениями, которые помогут нам проверить наши формулы. Используйте известную информацию из нашего примера компакт-диска (см. изображение ниже). 9(1/(В14*В16))-1)
3. В ячейку B20 введите =LOG(B15/B12)/(B16*LOG(1+(B13/B16)))
4. Желтые ячейки должны были автоматически заполниться 1000 долларов США для основной суммы, 0,0144 для ставки и 5 для лет. Если они этого не сделали, возможно, вы допустили ошибку при вводе формулы. Внимательно проверьте наличие всех скобок! Внесение формул в электронную таблицу один раз может быть утомительной работой, но в долгосрочной перспективе это сэкономит время, если вы будете использовать таблицу неоднократно.
5. Остальные ячейки для сложных процентов нам не понадобятся. Вы можете полностью удалить эти строки, щелкнув номер первой строки, перетащив вниз, чтобы включить их все, щелкнув правой кнопкой мыши и выбрав «Удалить». Калькулятор сложных процентов готов!

Шаг 2: Воспользуйтесь калькулятором

Воспользуйтесь калькулятором, чтобы исследовать следующие ситуации.

пример

Предположим, вы вносите 7 395 долларов США в депозитный сертификат сроком на 3 года с ежемесячной процентной ставкой 0,9%.

(a) Сколько денег будет у вас на счету, когда компакт-диск созреет?

(b) Сколько всего процентов вы заработаете?

(c) Если в день погашения вы реинвестируете остаток на счете в депозитный сертификат сроком на 5 лет с выплатой 1,29проценты, начисляемые ежедневно, сколько денег будет у вас на счете, когда наступит срок погашения второго компакт-диска?

(d) Насколько вырастут ваши первоначальные инвестиции в размере 7 395 долларов США за 8 лет инвестирования?

Решение

 

Пример

У вас есть 20 000 долларов из наследства. Вы хотели бы вложить хотя бы часть из них в компакт-диск.

(a) Вы нашли компакт-диск с выплатой 1,39%, начисляемой ежедневно в течение 3 лет. Какую сумму вам нужно внести, если вы хотите, чтобы баланс счета составлял 10 000 долларов США

(b) Какую ставку вам нужно получить, чтобы увеличить все 20 000 до 25 000 долларов за 10 лет? Можно предположить ежедневное начисление процентов.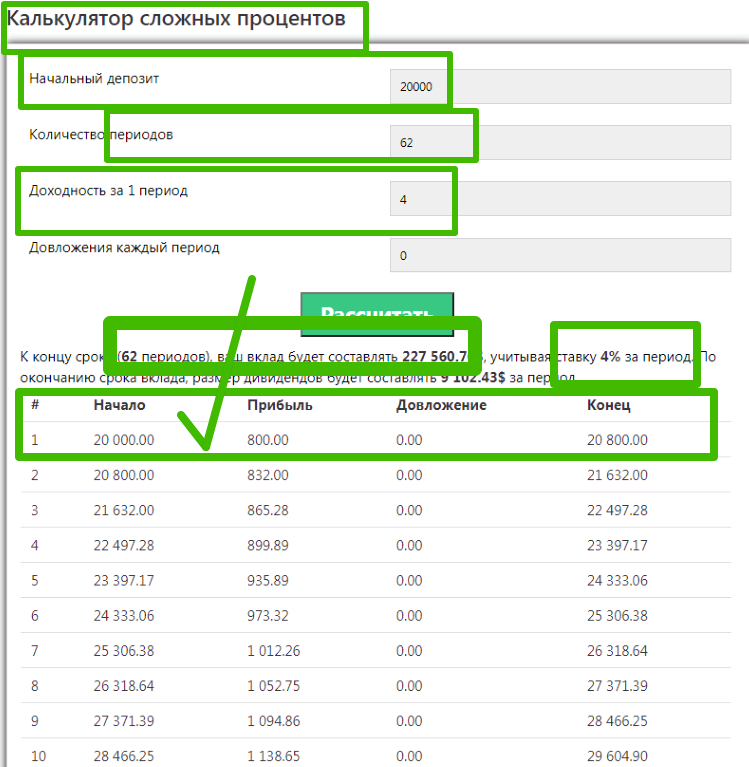

(c) Если вы хотите потратить 5 000 долларов сейчас, но хотите, чтобы оставшиеся 15 000 долларов в конечном итоге выросли до 20 000 долларов, какой срок погашения вам потребуется для депозитного сертификата, выплачивающего 1,89% в день?

Решение

 

попробуйте

 

Сложные проценты | Математика для гуманитарных наук Corequisite

Результаты обучения

• Расчет сложных процентов с учетом процентного сценария
• Рассчитать начальный баланс с учетом процентного сценария
• Решить время в задаче на сложные проценты

Начисление сложных процентов

С простыми процентами мы предполагали, что мы присвоили проценты, когда мы их получили. На стандартном банковском счете любые проценты, которые мы зарабатываем, автоматически добавляются к нашему балансу, и мы получаем проценты на эти проценты в последующие годы. Это реинвестирование процентов называется рецептура .

Предположим, что мы вносим 1000 долларов на банковский счет с процентной ставкой 3%, начисляемой ежемесячно. Как будут расти наши деньги?

Процентная ставка в размере 3% представляет собой годовую процентную ставку (годовые проценты) – общую сумму процентов, подлежащих выплате в течение года. Поскольку проценты выплачиваются ежемесячно, каждый месяц мы будем зарабатывать [latex]\frac{3%}{12}[/latex]= 0,25% в месяц.

В первый месяц

• P ₀ = 1000 долларов
• r = 0,0025 (0,25%)
• I = 1000 долл. США (0,0025) = 2,50 долл. США
• A = 1000 долл. США + 2,50 долл. США = 1002,50 долл. США

В первый месяц мы заработаем 2,50 доллара в виде процентов, увеличив баланс нашего счета до 1002,50 доллара.

Во втором месяце

• P ₀ = 1002,50 долл. США
• I = 1002,50 долл. США (0,0025) = 2,51 долл. США (округлено)
• А = 1002,50 долл. США + 2,51 долл. США = 1005,01 долл. США

Обратите внимание, что во второй месяц мы заработали больше процентов, чем в первый месяц. Это связано с тем, что мы заработали проценты не только на первоначальные 1000 долларов США, которые мы внесли, но мы также получили проценты на 2,50 доллара США процентов, которые мы заработали в первый месяц. Это ключевое преимущество начисление процентов  нам дают проценты.

Подсчет еще нескольких месяцев дает следующее:

Месяц	Начальный баланс	Полученные проценты	Конечный баланс
1	1000.00	2,50	1002.50
2	1002.50	2,51	1005.01
3	1005.01	2,51	1007.52
4	1007.52	2,52	1010. 04
5	1010.04	2,53	1012,57
6	1012,57	2,53	1015.10
7	1015.10	2,54	1017,64
8	1017,64	2,54	1020.18
9	1020.18	2,55	1022,73
10	1022,73	2,56	1025.29
11	1025.29	2,56	1027,85
12	1027,85	2,57	1030.42

Мы хотим упростить процесс расчета сложных процентов, поскольку создание таблицы, подобной приведенной выше, требует много времени. К счастью, математика хорошо подсказывает, как срезать путь. Чтобы найти уравнение, представляющее это, если P _m represents the amount of money after m months, then we could write the recursive equation:

P ₀ = $1000

P _m

= (1+0. 0025) P _м-1

Вы можете узнать это как рекурсивную форму экспоненциального роста.

рекурсивный рост

Вспомните основной процесс рекурсивного роста. Начиная с начального количества, [latex]P_0[/latex], каждое последующее количество, [latex]P_m[/latex], растет пропорционально себе, [latex]P_{m-1}[/latex], с некоторой скоростью. [латекс]г[/латекс]. 9{m+n}[/латекс].

То есть при умножении подобных оснований мы складываем показатели степени.

Пример

Постройте явное уравнение для роста 1000 долларов, размещенных на банковском счете с процентной ставкой 3%, с ежемесячным начислением сложных процентов.

Показать раствор

Посмотрите это видео, чтобы ознакомиться с концепцией сложных процентов.

Хотя эта формула работает нормально, чаще используется формула, включающая количество лет, а не количество периодов начисления сложных процентов.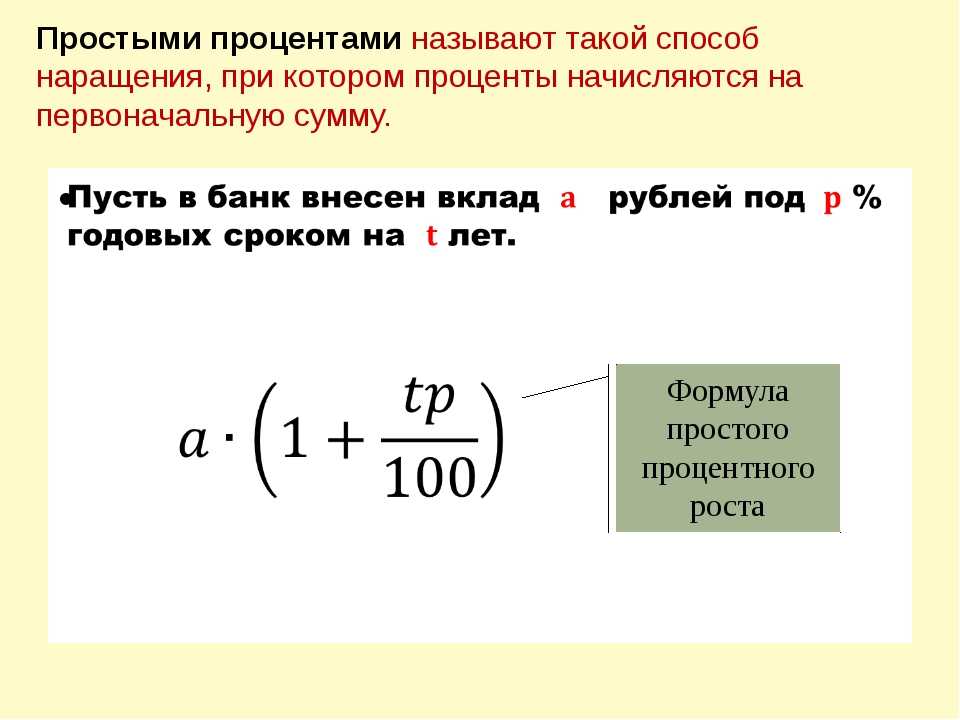 Если N количество лет, тогда м = N k . Это изменение дает нам стандартную формулу сложных процентов.

[латекс]m=Nk[/латекс]

Как мы получили [латекс]m = Nk[/латекс]?

Напомним, что [latex]m[/latex] представляет собой количество периодов начисления процентов, в течение которых инвестиция остается на счете, а [latex]k[/latex] представляет количество раз в год, когда ваши проценты начисляются. Если проценты по вашему депозиту начисляются ежемесячно, то [latex]k = 12[/latex]. Если оставить депозит на [latex]1[/latex] год, то [latex]m = 12[/latex]. Но если [latex]k = 12[/latex] и вы оставляете залог на [latex]2[/latex] лет, тогда [latex]m = 2*12 = 24[/latex]. Глядя на это с другой стороны, [латекс]м = N\текст{ лет} * к[/латекс].

[латекс]m = Nk[/латекс].

Пример. Инвестиции в размере 1000 долларов США, приносящие проценты по ставке 4%, начисляемые ежеквартально (4 раза в год), остаются на счете в течение [latex]3[/latex] лет.

У нас есть [латекс]4[/латекс] периода начисления процентов в год, поэтому [латекс]k = 4[/латекс]

Если мы оставим наши деньги на [латекс]1[/латекс] год, количество периоды начисления составляют [латекс]1*4: м=4[/латекс].

Если мы оставим наши деньги на [латекс]3[/латекс] лет, [латекс]m = 3*4[/латекс] или [латекс]12[/латекс]. 9{Nk}[/latex]

• P _N это остаток на счете после N лет.
• P ₀ — начальный баланс счета (также называемый начальным депозитом или основной суммой)
• r — годовая процентная ставка в десятичной форме
• k — количество периодов начисления сложных процентов в одном году.
  • Если начисление производится ежегодно (раз в год), к = 1.
  • Если начисление процентов производится ежеквартально, к = 4.
  • Если начисление процентов производится ежемесячно, k = 12.
  • Если начисление процентов производится ежедневно, k = 365.

Самое важное, что нужно помнить об использовании этой формулы, это то, что она предполагает, что мы кладем деньги на счет один раз и оставляем их там, чтобы получать проценты.

В следующем примере мы покажем, как использовать формулу сложных процентов, чтобы найти остаток по депозитному сертификату через 20 лет.

не забудьте преобразовать проценты в десятичную форму

Обычно для выполнения вычислений над числом, выраженным в процентах, вам необходимо преобразовать его в десятичную форму. Ставка [latex]r[/latex] в формулах процентов должна быть преобразована из процентов в десятичную форму перед использованием формулы.

Пример

Депозитный сертификат (CD) — это сберегательный инструмент, который предлагают многие банки. Обычно это дает более высокую процентную ставку, но вы не можете получить доступ к своим инвестициям в течение определенного периода времени. Предположим, вы вкладываете 3000 долларов в депозитный сертификат с ежемесячной процентной ставкой 6%. Сколько будет у вас на счету через 20 лет?

Показать решение

Видеообзор этого примера проблемы доступен ниже.

Давайте сравним сумму денег, заработанную на сложном проценте, с суммой, которую вы заработаете на простых процентах

Годы	Простые проценты (15 долларов США в месяц)	6% ежемесячно начисляется = 0,5% каждый месяц.
5	$3900	4046,55 $
10	4800 $	5458,19 $
15	$5700	7362,28 $
20	6600 $	9930,61 $
25	7500 $	13394,91 $
30	$8400	18067,73 $
35	$9300	24370,65 $

Как видите, в течение длительного периода времени начисление сложных процентов сильно влияет на баланс счета. Вы можете распознать в этом разницу между линейным ростом и экспоненциальным ростом.

Линейный рост против экспоненциального роста

Напомним, что линейный рост увеличивается с постоянной скоростью. График линейного роста будет описывать прямую линию между любыми двумя точками на графике. График изменяется на ту же аддитивную величину на единицу ввода.

Например, банковский счет, который увеличивается на 5 долларов в год, имеет линейный рост.

Экспоненциальный рост описывает количество, растущее со скоростью, пропорциональной самой себе на каждую единицу ввода. График изменяется кратно своему текущему значению на единицу ввода. График будет описывать быстро возрастающую кривую. 9{x}}\пробел 240[/латекс]. Попробуйте — у вас должно получиться что-то около 3.3102044758.

Пример

Вы знаете, что через 18 лет вам потребуется 40 000 долларов на образование вашего ребенка. Если ваш счет зарабатывает 4% ежеквартально, сколько вам нужно внести сейчас, чтобы достичь своей цели?

Показать раствор

Попробуй

Округление

Важно быть очень осторожным с округлением при вычислениях с показателями степени. В общем, вы хотите сохранить как можно больше десятичных знаков во время вычислений. Обязательно сохранить не менее 3 значащих цифр (числа после любых начальных нулей). Округление 0,00012345 до 0,000123 обычно дает «достаточно близкий» ответ, но всегда лучше оставить больше цифр.

Пример

Чтобы понять, почему недопустимость чрезмерного округления так важна, предположим, что вы инвестируете 1000 долларов под 5% годовых, начисляемых ежемесячно в течение 30 лет.

P 0 = 1000 долларов	первоначальный взнос
r = 0,05	5%
к = 12	12 месяцев в 1 году
N = 30	так как ищем сумму через 30 лет

Если мы сначала вычислим R/K , мы находим 0,05/12 = 0,00416666666667

Вот эффект от округления до различных значений:

09112570 70 91125.

Получается P 30 будет:	Ошибка
0,004	4208,59 $	259,15 $
0,0042	4521,45 $	53,71 $
0,00417	4473,09 $	5,35 $
0,004167	4468,28 $	0,54 $
0,0041667	4467,80 $	$0,06
без округления	4467,74 $

Если вы работаете в банке, вы, конечно, вообще не будете округлять. Для наших целей ответ, который мы получили, округлив до 0,00417, трех значащих цифр, достаточно близок — скидка 5 долларов с 4500 долларов не так уж и плоха. Конечно, сохранение этого четвертого знака после запятой не помешало бы.

Просмотрите следующее для демонстрации этого примера.

 

С помощью калькулятора 9{360}}[/латекс].



Теперь мы можем использовать калькулятор.

Введите этот	Калькулятор показывает
0,05 ÷ 12 = .	0,00416666666667
+ 1 = .	1,00416666666667
ух 360 = .	4.46774431400613
× 1000 = .	4467.74431400613

Использование калькулятора продолжение

Предыдущие шаги предполагали, что у вас есть калькулятор «одна операция за раз»; более продвинутый калькулятор часто позволяет вам ввести вычисляемое выражение целиком. Если у вас есть такой калькулятор, вам, вероятно, потребуется ввести:

1000 ×  ( 1 + 0,05 ÷ 12 ) y ^x 360 =

Решение для времени

Примечание. В этом разделе предполагается, что вы рассмотрели решение экспоненциальные уравнения с использованием логарифмов либо в предыдущих классах, либо в главе о моделях роста.